Electromagnetic Waves Class 12 Notes Physics Chapter 8 - CBSE

Chapter : 8

What are Electromagnetic Waves ?

https://drive.google.com/file/d/1b_H0ReA9I7s4u6s3l_kxthLN3z5EmRI6/view


Topic	Formula	Symbol Representation	Important Points
Displacement Current	$$\text{I}_\text{D}= \epsilon_\text{0}\frac{\text{d}\phi_\text{E}}{\text{dt}}\\ \space\space\space\space\space\space\text{or} \\ \frac{\text{dq}}{\text{dt}}=\epsilon_\text{0}\frac{\text{d}\phi}{\text{dt}}$$	I_D = Maxwell’s displacement current Φ = Electric flux (dΦ/dt) = Rate of change of electric flux	When electric field or electric flux change with time, ID comes in the picture. I_D does not exist in steady condition in a region. I_D does not flow through the conducting wire. I_D produce magnetic field in a region.
Electromagnetic waves	$$\text{c}=\frac{1}{\sqrt{\mu_0\epsilon_0}}\\=3×10^8\text{ms}^{-1}\\ \oint\vec{\text{B}}.\vec{\text{dl}}=\mu_0(\text{I}+\text{I}_\text{D})\\=\mu_0(\text{I}+\frac{\epsilon_0\text{d}\phi_\epsilon}{\text{dt}})\\ (\text{Ampere-Maxwell law}) \\ \oint\vec{\text{E}}\vec{\text{ds}}=\frac{\text{q}}{\epsilon_0}\\ \text{Gauss law in electrostate}$$ $$\oint\vec{\text{B}}.\vec{\text{ds}}=0\\ \text{(Gauss law in magnetostate)} \\ \oint\vec{\text{E}}.\vec{\text{dl}}=\frac{\text{-df}}{\text{dt}}\int_s \vec{\text{B}}\vec{\text{ds}} \\ \text{(Faraday’s law of EM induction)}$$	c = speed of light μ₀ = permeability constant = 4π × 10^-7H/m ε₀ = Vacuum permittivity = 8.85 × 10^-12C²/N.m² 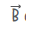= magnetic field ∮ = integral over closed path I = conduction current I_D = displacement current	$$\bull\space \text{Electric field} \vec{(\text{E})} \text{and magnetic field} \\\vec{(\text{B})} \text{are at right angle to each other}\\ \space \text{as well as right angle to the}\\ \text{direction of wave propagation}. $$ Example: radio waves, microwaves, infrared waves etc. Speed of EM, in vacuum, is equal to speed of light. Oscillating or accelerated charge produced EM. EM waves are transverse in nature (Maxwell). EM wave do not require any medium for propagation. $$\bull\space \vec{\text{E}} \space\text{and} \space\vec{\text{B}} \space\text{are in same phase (in EM)}. $$ Velocity of EM wave entirely depends on electric and magnetic field of medium. Energy carried by EM wave equally divide between $$\space \vec{\text{E}} \space\text{and} \space\vec{\text{B}}$$ EM waves are not deflected by electric and magnetic field.
EM spectrum			Orderly distribution of EM radiations according to their wavelength or frequency.