Electromagnetic Waves Class 12 Notes Physics Chapter 8 - CBSE

Chapter : 8

What are Electromagnetic Waves ?

The dot mark ◉ field are mandatory, So please fill them in carefully
To download the complete Syllabus (PDF File), Please fill & submit the form below.
https://drive.google.com/file/d/1b_H0ReA9I7s4u6s3l_kxthLN3z5EmRI6/view

    Topic Formula Symbol Representation Important Points
    Displacement Current $$\text{I}_\text{D}= \epsilon_\text{0}\frac{\text{d}\phi_\text{E}}{\text{dt}}\\ \space\space\space\space\space\space\text{or} \\ \frac{\text{dq}}{\text{dt}}=\epsilon_\text{0}\frac{\text{d}\phi}{\text{dt}}$$ ID = Maxwell’s displacement current
    Φ = Electric flux
    (dΦ/dt) = Rate of change of electric flux
    • When electric field or electric flux change with time, ID comes in the picture.

    • ID does not exist in steady condition in a region.

    • ID does not flow through the conducting wire.

    • ID produce magnetic field in a region.
    Electromagnetic waves $$\text{c}=\frac{1}{\sqrt{\mu_0\epsilon_0}}\\=3×10^8\text{ms}^{-1}\\ \oint\vec{\text{B}}.\vec{\text{dl}}=\mu_0(\text{I}+\text{I}_\text{D})\\=\mu_0(\text{I}+\frac{\epsilon_0\text{d}\phi_\epsilon}{\text{dt}})\\ (\text{Ampere-Maxwell law}) \\ \oint\vec{\text{E}}\vec{\text{ds}}=\frac{\text{q}}{\epsilon_0}\\ \text{Gauss law in electrostate}$$
    $$\oint\vec{\text{B}}.\vec{\text{ds}}=0\\ \text{(Gauss law in magnetostate)} \\ \oint\vec{\text{E}}.\vec{\text{dl}}=\frac{\text{-df}}{\text{dt}}\int_s \vec{\text{B}}\vec{\text{ds}} \\ \text{(Faraday’s law of EM induction)}$$    		 c = speed of light
    μ0 = permeability constant = 4π × 10-7H/m
    ε0 = Vacuum permittivity = 8.85 × 10-12C2/N.m2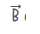
    Symbol Representation
    = magnetic field
    ∮ = integral over closed path
    I = conduction current
    ID = displacement current    		 $$\bull\space \text{Electric field} \vec{(\text{E})} \text{and magnetic field} \\\vec{(\text{B})} \text{are at right angle to each other}\\ \space \text{as well as right angle to the}\\ \text{direction of wave propagation}. $$
    Example: radio waves, microwaves, infrared waves etc.
    • Speed of EM, in vacuum, is equal to speed of light.

    • Oscillating or accelerated charge produced EM.

    • EM waves are transverse in nature (Maxwell).

    • EM wave do not require any medium for propagation.

      • $$\bull\space \vec{\text{E}} \space\text{and} \space\vec{\text{B}} \space\text{are in same phase (in EM)}. $$
    • Velocity of EM wave entirely depends on electric and magnetic field of medium.

    • Energy carried by EM wave equally divide between

      • $$\space \vec{\text{E}} \space\text{and} \space\vec{\text{B}}$$
  • EM waves are not deflected by electric and magnetic field.
    		•
    EM spectrum
  • Orderly distribution of EM radiations according to their wavelength or frequency.
    		•