NCERT Solutions for Class 10 Maths Chapter 2 - Polynomials

NCERT Solutions for Class 10 Mathematics Chapter 2 Free PDF Download

Please Click on Free PDF Download link to Download the NCERT Solutions for Class 10 Mathematics Chapter 2 Polynomials

https://drive.google.com/file/d/1pNM_6TFuchVbmwTiMLMy7AR-353AwsaP/view?usp=sharing

Exercise 2.1

1. The graphs of y = p(x) are given in figures below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

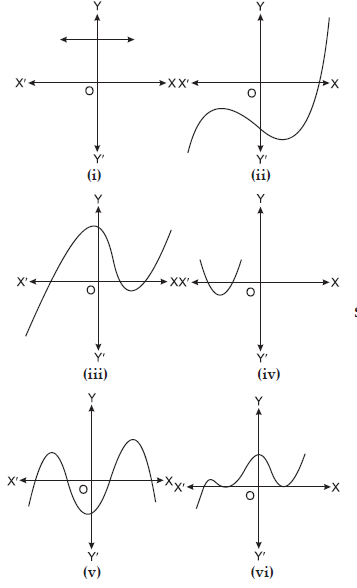
Sol. (i) The graph do not intersects the x-axis.
Then Number of zeroes = No zeroes.
(ii) The graph intersects the x-axis at one point only.
Then Number of zeroes = 1
(iii) The graph intersects the x-axis at three points.
Then Number of zeroes = 3
(iv) The graph intersects the x-axis at two points.
Then Number of zeroes = 2
(v) The graph intersects the x-axis at four points.
Then Number of zeroes = 4
(vi) The graph intersects the x-axis at three points.
Then Number of zeroes = 3

Exercise 2.2

1. Find the zeroes of the following quadratic polynoials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² – 3 – 7x
(vi) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4

Sol. (i) Let be
F(x) = x² – 2x – 8
F(x) = x² – 4x + 2x – 8
F(x) = x(x – 4) + 2(x – 4)
F(x) = (x – 4)(x + 2)
So, the value of x² – 2x – 8 is zero.
F(x) = 0
(x – 4)(x + 2) = 0
When
x – 4 = 0, x = 4
x + 2 = 0, x = – 2
Therefore, the zeroes of x² – 2x – 8 are 4
and – 2
Now,
Sum of zeroes = 4 + (– 2)
= 2

$$\text{Sum of zeroes}=\frac{−(coefficient of x)}{−(coefficient of x^2)}\\=\frac{-(-2)}{1}\\=2\\\text{Product of zeroes} = 4 × – 2 = – 8\\\text{Product of zeroes}=\frac{\text{constant term}}{\text{termcoefficient of}\space x^2}\\=\frac{-8}{1}\\=-8$$

(ii) Let be F(s) = 4s² – 4s + 1
F(s) = 4s² – 2s – 2s + 1
= 2s(2s – 1) – 1(2s – 1)
= (2s – 1)(2s – 1) The value of F(s) = 0
(2s – 1)(2s – 1) = 0

$$(2s – 1) = 0, s =\frac{1}{2}\\(2s – 1) = 0, s =\frac{1}{2}\\\text{Therefore, the zeroes of}\space4s^2– 4s + 1\space are\space and\space\frac{1}{2}\\\text{Sum of zeroes} =\frac{1}{2}+\frac{1}{2}=1\\\text{Sum of zeroes}=\frac{−(coefficient of S)}{(coefficient of S^2)}\\=\frac{-(-4)}{4}=1\\\text{Product of zeroes}=\frac{1}{2}×\frac{1}{2}=\frac{1}{4}\\\text{Product of zeroes}=\frac{\text{constant term}}{\text{coefficient of} \space S^2}\\=\frac{1}{4}\\\text{Relationship between the zeroes and the coefficients is true.}$$

(iii) Let be
F(x) = 6x² – 3 – 7x
⇒ F(x) = 6x² – 7x – 3
⇒ F(x) = 6x² – 9x + 2x – 3
⇒ F(x) = 3x(2x – 3) + 1(2x – 3)
⇒ F(x) = (2x – 3)(3x + 1)
Value of F(x) = 0
⇒ (2x – 3)(3x + 1) = 0
⇒ 2x – 3 = 0, 3x + 1 = 0
⇒ 2x = 3, 3x = – 1

$$x=\frac{3}{2},\space\space\space\space\space\space\space\space\space\space x=\frac{-1}{3},\\\text{Therefore, the zeroes of}\space 6x^2 – 3 – 7x\space\text{are}\frac{3}{2}\space\text{and}\space\frac{-1}{3}\\\text{Sum of zeroes}=\frac{3}{2}+(\frac{-1}{3})\\=\frac{9-2}{6}=\frac{7}{6}\\\text{Sum of zeroes}=\frac{\text{−(coefficient of x)}}{\text{(coefficient of}\space x^2)}\\=\frac{-(-7)}{6}\\=\frac{7}{6}\\\text{Product of zeroes}=\frac{3}{2}×\frac{-1}{3}\\=-\frac{1}{2}\\\text{Relationship between the zeroes and the coefficients is true.}$$

(iv) Let be
F(u) = 4u² + 8u
⇒ F(u) = 4u (u + 2)
The value of F(u) = 0
⇒ 4u(u + 2) = 0
⇒ 4u (u + 2) = 0
⇒ 4u = 0, u + 2 = 0
⇒ u = 0, u = – 2
Therefore, the zeroes of 4u² + 8u are 0 and – 2.
Now
sum of zeores = 0 + (– 2) = – 2

$$\text{Sum of zeroes}=\frac{\text{−(coefficient of u)}}{\text{(coefficient of}\space u^2)}\\=\frac{8}{4}=-2\\\text{Sum of zeroes}= 0 × – 2 = 0\\\text{Sum of zeroes}=\frac{\text{constant term}}{\text{term coefficient of}\space u^2}\\=\frac{0}{4}=0\\\text{Relationship between the zeroes and the coefficients is true.}$$

(v) Let be
F(t) = t² – 15
The value of F(t) = 0
t² – 15 = 0
(t²-√ 15²)=0
(t-√ 15)(t+√ 15)=0
Then,
t−√ 15 = 0
t+√ 15 = 0
t = √15
t = -√15
Therefore, the zeroes of t² – 15 are √15 and −√15.
Sum of zeroes = √15−√15= 0
$$\text{Sum of zeroes}=\frac{\text{−(coefficient of t)}}{\text{(coefficient of}\space t^2)}\\=\frac{-0}{1}=0\\\text{Product of zeroes}= \sqrt[]{15}×-\sqrt[]{15}=-15\\\text{Product of zeroes}=\frac{\text{constant term}}{\text{coefficient of}\space t^2}\\=\frac{-15}{1}=-15\\\text{Relationship between the zeroes and the coefficients is true.}$$

(vi) Let be
F(x) = 3x² – x – 4
F(x) = 3x² – 4x + 3x – 4
F(x) = x(3x – 4) + 1(3x – 4)
F(x) = (3x – 4)(x + 1)
So, the value of F(x) is zero.
F(x) = 0
(3x – 4)(x + 1) = 0
3x – 4 = 0, x + 1 = 0
3x = 4, x = – 1
x=4/3
$$\text{Therefore, the zeroes of the}\space 3x^2 – x – 4\text{are}\frac{4}{3}\text{and}-1\\\text{Sum of zeroes}=\frac{4}{3}+(-1)\\\frac{4-3}{3}\\=\frac{1}{3}\\\text{Sum of zeroes}=\frac{\text{−(coefficient of x)}}{\text{(coefficient of}\space x^2)}\\=\frac{-(-1)}{3}=\frac{1}{3}\\\text{Product of zeroes}=\frac{4}{3}×-1\\=\frac{-4}{3}\\\text{Product of zeroes}=\frac{\text{(coefficient of x)}}{\text{(coefficient of}\space x^2)}\\\text{Product of zeroes}=\frac{-4}{3}\\\text{Relationship between zeroes and coefficients are true.}$$

2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
$$(i)\frac{1}{4},-1\\(ii)\sqrt{2},\frac{1}{3}\\(iii)0,\sqrt{5}\\(iv)1,1\\(v)\frac{-1}{4},\frac{1}{4}\\(vi)4,1$$

Sol. (i) Given that,
Sum of zoeres = 1/4
Product of zeroes = – 1
Quadratic polynomial is
x² – (sum of zeroes)x + product of zeroes = 0
$$x^2-\frac{1}{4}×x+(-1)=0\\\frac{4x^2-x-4}{4}=0\\4x^2-x-4=0\\\text{Hence, the Quadratic polynomial is}\\F(x) =4x^2-x-4.$$

$$(ii)\text{Given that,}\\\text{Sum of zeroes}=\sqrt{2}\space\text{and}\\\text{Product of zeroes}=\frac{1}{3}\\\text{Quadratic polynomial is :}\\x^2 –\text{(sum of zeroes)x + product of zeroes = 0}\\x^2-\sqrt{2x}+\frac{1}{3}=0\\{3x^2-3\sqrt{2x}+1=0}\\\text{Hence, the polynomial is :}\\F(x) ={3x^2-3\sqrt{2x}+1=0}$$

(iii) Given that,
Sum of zeroes = 0
Product of zeroes = √ 5
Quadraitc polynomial
x² – (sum of zeroes)x + product of zeroes = 0
x²-0 × X+√ 5 0
x²+√ 5=0
Hence, the polynomial is
F(x) =x²+√ 5

(iv) Given that,
Sum of zeroes = 1
Product of zeroes = 1
Quadratic polynomial is
x² – (sum of zeroes)x + product of zeroes = 0
x² – x + 1 = 0
Quadratic polynomial is :
F(x) = x² – x +1

$$(v) \text{Given that,}\\\text{Sum of zeroes}=\frac{-1}{4}\\\text{Product of zeroes}=\frac{1}{4}\\\text{Quadratic polynomial is}\\\text{x2 – (sum of zeroes)x + product of zeroes = 0}\\x^2-(\frac{-1}{4})x+\frac{1}{4}=0\\x^2+\frac{x}{4}+\frac{1}{4}=0\\\frac{4x^2+x+1}{4}=0\\4x^2 + x + 1 = 0\\4x^2 + x + 1 = 0\\\text{Hence, the polynomial is}\\ F(x) = 4x^2 + x + 1$$

(vi) Given that,
Sum of zeroes = 4
Product of zeroes = 1
Quadratic polynomial is
x² – (sum of zeroes)x + product of zeroes = 0
x² – 4x + 1 = 0
Hence, the polynomial is
F(x) = x² – 4x + 1.

Exercise 2.3

1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²

Sol. (i) P(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
x² – 2 ) x³ – 3x² + 5x – 3 (x – 3
x³ – 2x
$$x^3-2x\\\frac{-\space\space\space\space\space\space\space +}{– 3x^2 + 7x – 3}\text{By subtract}\\– 3x^2 + 6\\\frac{+\space\space\space\space\space\space\space -}{7x – 9}\text{By subtract}$$
Quotient q(x) = x – 3
Remainder R(x) = 7x – 9

(ii) p(x) = x⁴ – 3x² + 4x + 5
g(x) = x² + 1 – x
Rearranging g(x)
g(x) = x² – x + 1
x² – x + 1 ) x⁴ – 3x² + 4x + 5 (x² + x – 3
x⁴ – x³ + x²

$$\frac{-\space\space\space+\space\space\space\space -}{x^3 – 4x^2 + 4x + 5}\text{By subtract}\\x^3 – x^2 + x\\\frac{-\space\space\space\space+\space\space\space\space -}{– 3x^2 + 3x + 5}\\– 3x^2 + 3x + 5\\\frac{+\space\space\space\space-\space\space\space\space +}{8}\text{By subtract}\\\text{Quotient q(x)} = x^2 + x – 3\\\text{Remainder r(x)} = 8$$

(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
– x² + 2) x⁴ – 5x + 6 (– x² – 2
x⁴ – 2x²

$$\frac{- \space\space\space\space+}{2x^2–5x+6}\\2x^2–4\\\frac{-\space\space\space\space +}{–5x+10}\\\text{Quotient q(x)} = – x^2 – 2\\\text{Remainder R(x)} = – 5x + 10$$

2. Check whether the first polynomial is a factor of the second polynoial by dividing the second polynomial by the first polynomial
(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x4 + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

Sol. (i) Let be
I Polynomial p(t) = t² – 3
II Polynomial q(t) = 2t⁴+ 3t³ – 2t² – 9t – 12
t² – 3) 2t⁴ + 3t³ – 2t² – 9t – 12 (2t² + 3t + 4
2t⁴– 6t²

$$\frac{- \space\space\space\space+}{3t^3 + 4t^2 – 9t – 12}\\3t^3 – 9t\\\frac{-\space\space\space\space +}{4t^2 – 12}\\4t^2 – 12\\\frac{-\space\space\space\space +}{0}\\\text{Remainder }= 0\\\text{Then First polynomial is a factor of the second polynomial.}$$

(ii) Let be
I polynomial p(x) = x² + 3x + 1
II polynomial q(x) = 3x⁴ + 5x³ – 7x² + 2x + 2
x² + 3x + 1) 3x⁴ + 5x³ – 7x² + 2x + 2 (3x² – 4x + 2
3x⁴ + 9x³ + 3x²

$$\frac{- \space\space-\space\space-}{-4x^3 + 10x^2 +2x +2}\\-4x^3 – 12x^2-4x\\\frac{-\space\space-\space\space -}{2x^2 +6x+2}\\2x^2 +6x+2\\\frac{-\space\space-\space\space -}{0}\\\text{Remainder }= 0\\\text{Therefore First polynomial is a factor of the second polynomial.}$$

(iii) Let be
I Polynomial p(x) = x³ – 3x + 1
II Polynomial q(x) = x⁵ – 4x³ + x² + 3x + 1
x³ – 3x + 1) x⁵ – 4x³ + x² + 3x + 1 (x² – 1
x⁵ – 3x³ + x²

$$\frac{- \space\space+\space\space-}{-x^3 +3x +1}\\-x^3 +3x+1\\\frac{+\space\space-\space\space +}{2}\\\text{Remainder }= 2\\\text{Therefore,}\\\text{ First polynomial is not a factor of the second polynomial.}$$

3. Obtain all other zoroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are √5/3 and -√ 5/3

$$\text{Sol. Since two zeroes are}\space\sqrt{\frac{5}{3}}\space\text{and}-\space\sqrt{\frac{5}{3}}\\\Biggl(x-\sqrt{\frac{5}{3}}\Biggr)\Biggl(x+\sqrt{\frac{5}{3}}\Biggr)\\=x^2-\frac{5}{3}\\\text{is a factor of the given polynomial. Now, we divide the given polynomial by}\space x^2-\frac{5}{3}\\ x^2-\frac{5}{3}\Biggr)3x^4+6x^3-2x^2-10x-5\Biggl(3x^2+6x+3\\3x^2-5x^2\\\frac{- \space\space\space\space+}{6x^3 +3x^2 -10x-5}\\6x^3 -10x\\\frac{-\space\space\space\space +}{3x^2-5}\\3x^2-5\\\frac{- +}{0}\\\text{so,}3x^4 + 6x^3 – 2x^2 – 10x – 5\\=\Biggl(x^2-\frac{5}{3}\Biggr)(3x^2+6x+3)\\\text{We factorise}(3x^2+6x+3)\\3x^2 + 6x + 3 = 3x^2 + 3x + 3x + 3\\= 3x (x + 1) + 3(x + 1)\\= (x + 1)(3x + 3)\\\text{So, its zeroes are given by x = – 1 and x = – 1. Therefore, the zeroes of the given} \\\text{polynomial are}\space\sqrt{\frac{5}{3}},-\sqrt{\frac{5}{3}}\space– 1 and – 1 .$$

4. On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4, respectively. Find g(x).

Sol. We know that
Dividend = Divisor × Quotient + Remainder
Given
Dividend = x³ – 3x² + x + 2 Divisor = g(x) = ?
Quotient = x – 2
Remainder = – 2x + 4
Then
x³ – 3x² + x + 2 = g(x) × (x – 2) + (– 2x + 4)
x³ – 3x² + x + 2 = g(x) × (x – 2) – 2x + 4
g(x)(x – 2) = x³ – 3x² + x + 2 + 2x – 4
g(x) = x³ – 3x² + 3x – 2

$$g(x)=\frac{x^3-3x^2+3x-2}{x-2}\\x – 2) x^3 – 3x^2 + 3x – 2 (x^2 – x + 1\\x^3-2x^2\\\frac{-\space\space\space\space+}{-x^2 +3x-2}\\-x^2 +2x\\\frac{+\space\space\space\space -}{3x^2-5}\\3x^2-5\\\frac{+ -}{x-2}\\x-2\\\frac{- +}{0}\\g(x) = x^2 – x + 1$$

5. Given examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0

Sol. (i) p(x) = 3x³+ 6x² + 9x + 12
g(x) = 3
3) 3x³ + 6x² + 9x + 12 (x³ + 2x² + 3x + 4
3x²

$$\frac{-}{6x^2 +3x+12}\\6x^2\\\frac{-}{9x+12}\\9x\\\frac{-}{12}\\12\\\frac{-}{0}\\q(x) = x^3 + 2x^2 + 3x + 4, r(x) = 0\\\text{deg p(x) = deg q(x)}$$

(ii) p(x) = x⁴ + x³ + x + 4, g(x) = x³
x³ ) x⁴ + x³ + x + 4 ( x + 1
x⁴

$$\frac{-}{x^3 +x+4}\\x^3\\\frac{-}{x+4}\\q(x) = x + 1, r(x) = x + 4\\\text{deg q(x) = deg r(x)}$$

(iii) p(x) = x⁴ + 2, g(x) = x + 1
x + 1 ) x⁴ + 2 ( x³ – x² + x – 1
x⁴ + x³

$$\frac{-\space-}{-x^3 +2}\\-x^3-x^2\\\frac{+\space-}{x^2+2}\\x^2+x\\\frac{-\space-}{-x+2}\\-x-1\\\frac{+ +}{3}\\q(x) = x3 – x2 + x – 1\\r(x) = 3\\\text{deg r(x) = 0}$$

Exercise 2.4

1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case :
(i) 2x³ + x² – 5x + 2; 1212,,−
(ii) x³ – 4x² + 5x – 2; 2, 1, 1

Sol. (i) Let
P(x) = 2x³ + x² – 5x + 2

$$p\biggl(\frac{1}{2}\biggr)=2×\biggl(\frac{1}{2}\biggr)^3+\biggl(\frac{1}{2}\biggr)^2-5×\frac{1}{2}+2\\=2×\frac{1}{8}+\frac{1}{4}-\frac{5}{2}+2\\=\frac{1}{2}-\frac{5}{2}\\=0\\P(1) = 2 × 1^3 + 1^2 – 5 × 1 + 2\\= 2 × 1 + 1 – 5 + 2\\= 5 – 5\\=0\\P(– 2) = 2 × (– 2)^3 + (– 2)^2 – 5 × (– 2) + 2\\= – 16 + 4 + 10 + 2\\= – 16 + 16\\= 0\\Hence,\frac{1}{2},1\text{and – 2 are zeroes of polynomial P(x). According to question,}\\a = 2, b = 1, c = – 5, d = 2\\\text{Zeroes}, α =\frac{1}{2},β= 1, γ = – 2.\\\text{Therefore,}\\α + β + γ =\frac{-b}{a}\\\frac{1}{2}+1-2=\frac{-1}{2}\\\frac{-1}{2}=\frac{-1}{2}\\αβ + βγ + γα =\frac{c}{a}\\\frac{1}{2}×1+1×(-2)+(-2)×\frac{1}{2}=\frac{-5}{2}\\\frac{1}{2}-2-1=\frac{-5}{2}\\\frac{1}{2}-3=\frac{-5}{2}\\\frac{-5}{2}=\frac{-5}{2}\\\text{And,}\\αβγ =\frac{-d}{a}\\\frac{1}{2}×1×(-2)=\frac{-2}{2}\\– 1 = – 1\\\text{Relationship between the zeroes and the coefficients in each case is true.}$$

(ii) Let P(x) = x³ – 4x² + 5x – 2
P(2) = 2³ – 4 × 2² + 5 × 2 – 2
P(2) = 8 – 16 + 10 – 2
P(2) = 0
P(1) = 1³ – 4 × 1² + 5 × 1 – 2
P(1) = 1 – 4 + 5 – 2
= 0
Hence, 2, 1 and 1 are zeroes of polynomial P(x).
According to question,
a = 1, b = – 4, c = 5, d = – 2
α= 2, β = 1, γ = 1
Now

$$α + β + γ =\frac{-b}{a}\\2 + 1 + 1 =\frac{-(-4)}{1}\\4 = 4\\\text{Again}\\αβ + βg + γα=\frac{c}{a}\\2 × 1 + 1 × 1 + 1 × 2=\frac{5}{1}\\2 + 1 + 2\\5 = 5\\\text{And,}\\αβγ =\frac{-d}{a}\\2 × 1 ×1 =\frac{-(-2)}{1}\\2 = 2\\\text{Relationship betw een the zeroes and the coefficients in each case is true.}$$

2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time and the product of its zeroes as 2, – 7, – 14 respectively.

Sol. Let be cubic polynomial
P(x) = ax³ + bx² + cx + d and its zeroes are α,βandγ .
Then according to question
α + β +γ = 2
$$\frac{-b}{a}=2\\a = 1, b = – 2\\αβ + βγ + γα =-7\\\frac{c}{a}=-7\\c = – 7a\\a = 1, c = – 7\\αβγ = – 14\\\frac{-d}{a}=-14\\d = 14\\\text{Put the value of a, b, c and d in polynomial P(x).}\\P(x) = x^3 – 2x^2 – 7x + 14$$

3. If the zeroes of the polynomial x3 – 3x2 + x + 1 are a – b, a, a + b find a and b.

Sol. Given Polynomial
P(x) = x³ – 3x² + x + 1
Compare
with Ax³ + Bx² + Cx + D
Then
A = 1, B = – 3, C = 1, D = 1
Given,
α = a – b, β= a, γ = a + b
We know that

$$α + β + γ =\frac{-B}{A}\\a – b + a + a + b =\frac{+3}{1}\\3a = 3\\a = 1\\α β γ =\frac{-D}{A}\\(a – b) × a × (a + b) =\frac{-1}{1}\\(a^2 – b^2) × a = – 1\text{Put the value of a}\\(1^2 – b^2) × 1 = – 1\\1 – b^2 = – 1\\– b^2 = – 2\\b^2 = 2\\b = ±\sqrt{2}$$

4. If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2±√ 3, find other zeroes.

Sol. Since, two zeroes are 23+ and 2+√ 3 and 2-√ 3,(x-2-√ 3 )(x-2+√ 3 )=x² – 4x + 1 is a factor of the given polynomial. Now, we divide the given polynomial x² – 4x + 1.
x² – 4x + 1 ) x⁴ – 6x³ – 26x² + 138x – 35 (x² – 2x – 35
x⁴ – 4x³ + x²

$$\frac{-+-}{– 2x^3 – 27x^2 + 138x – 35}Subtract\\– 2x^3 + 8x^2 – 2x\\\frac{+-+}{– 35x^2 + 140x – 35}Subtract\\– 35x^2 + 140x – 35\\\frac{+-+}{0}Subtract\\So,\\ x^4 – 6x^3 – 26x^2 + 138x – 35 = (x^2 – 4x + 1)(x^2 – 2x – 35)\\\text{We factorise}x^2 – 2x – 35 as (x – 7)(x + 5).\\\text{So, its zeroes are given by x = 7 and x = – 5.}\\\text{Therefore,the zeroes of the given polynomial are}\\2+\sqrt{3},2- \sqrt{3}\space\text{and} – 5.$$

5. If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k,the remainder comes out to be x + a, find k and a.

Sol. x² – 2x + k ) x⁴ – 6x³ + 16x² – 25x + 10 ( x² – 4x + (8 – k)
x⁴ – 2x³ + kx²

$$\frac{-+-}{– 4x^3 + (16 – k)x^2 – 25x + 10}\\– 4x^3 + 8x^2 – 4kx\\\frac{+-+}{(16 – k – 8)x^2 + (4k – 25)x + 10}\\(8 – k)x^2 + (4k – 25)x + 10\\(8 – k)x^2 – 2(8 – k)x + k(8 – k)\\\frac{-+-}{(4k – 25 + 16 – 2k)x + 10 – k(8 – k)}\\$$

(2k – 9)x + 10 – k(8 – k)
Quotient q(x) = x² – 4x + (8 – k)
Remainder r(x) = (2k – 9)x + 10 – k(8 – k)
Given remainder r(x) = x + a
Compare both remainder
2k – 9 = 1
2k = 10
k = 5
but
a = 10 – k(8 – k)
Put k = 5
⇒ a = 10 – 5(8 – 5)
⇒ a = 10 – 5 × 3
⇒ a = 10 – 15
⇒ a = – 5.
Hence, k = 5 and a = – 5.