Introduction To Trigonometry Class 10 Notes Maths: Chapter 8

The dot mark ◉ field are mandatory, So please fill them in carefully
To download the complete Syllabus (PDF File), Please fill & submit the form below.
https://drive.google.com/file/d/1vfHM9rpB6bnNVo2csYKTI0_qzR3rVuCT/view

    Basic Concepts-01

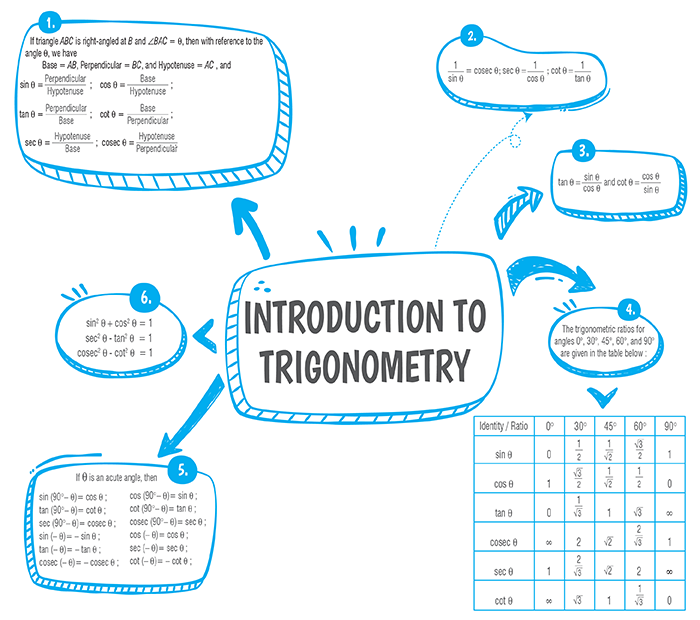
    Introduction Totrigonometry

    • If triangle ABC is right-angled at B and ∠BAC = θ, then with reference to the angle θ, we have Base = AB, Perpendicular = BC, and Hypotenuse = AC , and

    $$sin\space\theta=\frac{Perpendicular}{{Hypotenuse}}:cos\space\theta=\frac{Base}{{Hypotenuse}}:\\tan\space\theta=\frac{Perpendicular}{{Base}}:cot\space\theta=\frac{Base}{{Hypotenuse}}:\\sec\space\theta=\frac{Hypotenuse}{{Base}}:coses\space\theta=\frac{Hypotenuse}{{Perpendicular}}$$

    • $$\frac{1}{{sin\space\theta}}\space cosec\space\theta ;sec\space\theta= \frac{1}{{cos\space\theta}} ;cot\space\theta= \frac{1}{{tan\space\theta}}$$
    • $$tan\space\theta= \frac{sin\space\theta}{{cos\space\theta}}\space and \space cot\space\theta=\frac{cos\space\theta}{{sin\space\theta}}$$
    • The trigonometric ratios for angles 0°, 30°, 45°, 60°, and 90° are given in the table below :
    Identity / Ratio 0° 30° 45° 60° 90°
    sin θ 0 1/2 1/√2 √3/2 1
    cos θ 1 √3/2 1/√2 1/2 0
    tan θ 0 1/√3 1 √3 ∞
    cosec θ ∞ 2 √2 2/√3 1
    sec θ 1 2/√3 √2 2 ∞
    cot θ ∞ √3 1 1/√3 0
    • if θ is an acute angle, then
    sin (90°− θ)= cos θ ; cos (90°− θ)= sin θ ;
    tan (90°− θ)= cot θ ; cot (90°− θ)= tan θ ;
    sec (90°− θ)= cosec θ ; cosec (90°− θ)= sec θ ;
    sin (− θ)= − sin θ ; cos (− θ)= cos θ ;
    tan (− θ)= − tan θ ; sec (− θ)= sec θ ;
    cosec (− θ)= − cosec θ ; cot (− θ)= − cot θ ;
    • sin2 θ + cos2 θ = 1
      sec2 θ - tan2 θ = 1
      cosec2 θ - cot2 θ = 1