NCERT Solutions for Class 12 Maths Chapter 12 - Linear Programming - Exercise 12.2



Access Exercises of Class 12 Maths Chapter 12 – Linear Programming
Exercise 12.1 Solutions 10 Questions
Exercise 12.2 Solutions 11 Questions
Miscellaneous Exercise On Chapter 12 Solutions 10 Questions
Exercise 12.2
1. Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain atleast 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹ 60 per kg and food Q costs ₹ 80 per kg. Food P contains 3 units /kg of vitamin A and 5 units /kg of vitamin B while food Q contains 4 units /kg of vitamin A and 2 units /kg of vitamin B. Determine the minimum cost of the mixture.
Sol. Let Reshma mixes x kg of food P and y kg of food Q.
The required table is :
| Food | Quantity | Vitamin A | Vitamin B | Cost (₹ per kg) |
| P | x kg | 3x | 5x | 60x |
| Q | y kg | 4y | 2y | 80y |
| Total | 3x + 4y | 5x + 2y | 60x + 80y | |
| Required | Atleast 8 | Atleast 11 |
The mixture must contains atleast 8 units of vitamin A and 11 units of vitamin B. Total cost Z of purchasing food is Z = 60x + 80y.
The mathematical formulation of the given problem is
Minimize Z = 60x + 80y ...(i)
Subject to the constraints
3x + 4y ≥ 8 ...(ii)
5x + 2y ≥ 11 ...(ii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
3x + 4y = 8
| x | 0 | 8/3 |
| y | 2 | 0 |
Putting (0, 0) in the inequality 3x + 4y ≥ 8, we have
3 × 0 + 4 × 0 ≥ 8
⇒ 0 ≥ 8 (which is false)
So, the half plane is away from the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line
5x + 2y = 11
| x | 0 | 11/5 |
| y | 11/2 | 0 |
Putting (0, 0) in the inequality 5x + 2y ≥ 11, we have
5 × 0 + 2 × 0 ≥ 11
⇒ 0 ≥ 11 (which is false)
So, the half plane is away from the origin.

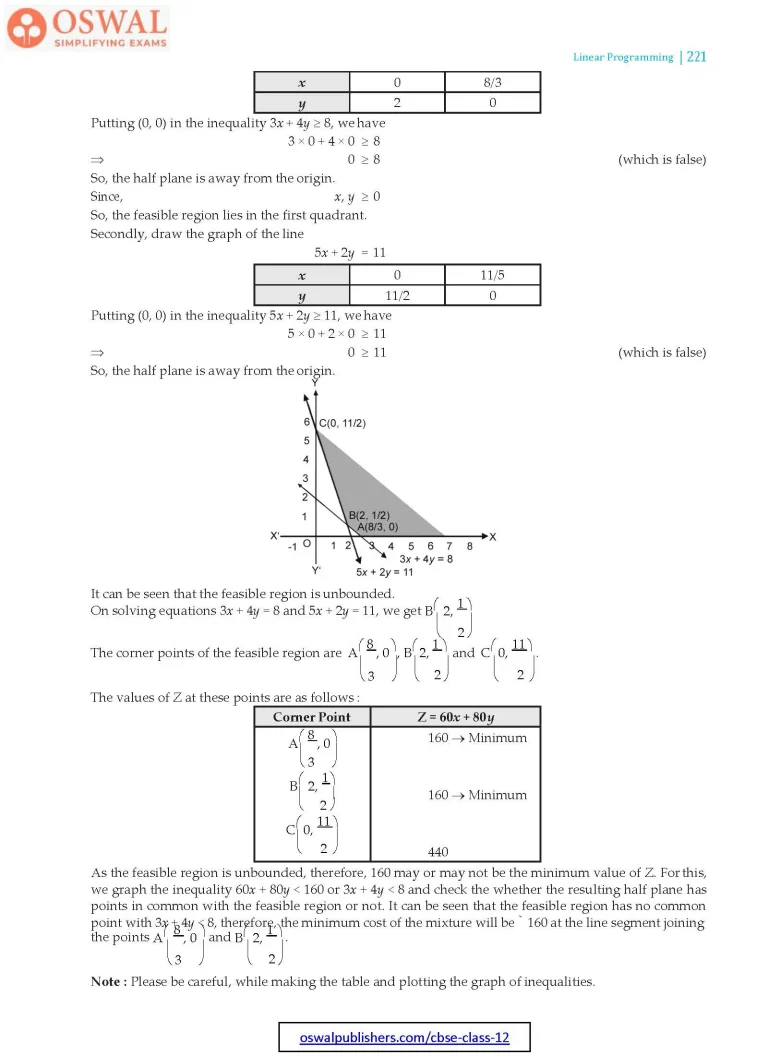
It can be seen that the feasible region is unbounded.
On solving equations 3x + 4y = 8 and 5x + 2y = 11,
$$\text{we get}\space\text{B}\bigg(2,\frac{1}{2}\bigg)$$
The corner points of the feasible region are
$$\text{A}\bigg(\frac{8}{3},0\bigg),\text{B}\bigg(2,\frac{1}{2}\bigg)\\\text{and}\space\text{C}\bigg(0,\frac{11}{2}\bigg).$$
The values of Z at these points are as follows :
| Corner Point | Z = 60x + 80y |
| $$\text{A}\bigg(\frac{8}{3},0\bigg)$$ | $$160\xrightarrow{}\text{Minimum}$$ |
| $$\text{B}\bigg(2,\frac{1}{2}\bigg)$$ | $$160\xrightarrow{}\text{Minimum}$$ |
| $$\text{C}\bigg(0,\frac{11}{2}\bigg)$$ | 440 |
As the feasible region is unbounded, therefore, 160 may or may not be the minimum value of Z. For this, we graph the inequality 60x + 80y < 160 or 3x + 4y < 8 and check the whether the resulting half plane has points in common with the feasible region or not. It can be seen that the feasible region has no common point with 3x + 4y < 8, therefore, the minimum cost of the mixture will be ₹ 160 at the line segment joining the points
$$A\bigg(\frac{8}{3},0\bigg)\text{and B}\bigg(2,\frac{1}{2}\bigg).$$
Note : Please be careful, while making the table and plotting the graph of inequalities.
2. One kind of cake requires 200 g of flour and 25 g of fat and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
Sol. Let the x be number of cakes of one kind and y be the number of cakes of other kind. Construct the following table :
| Kind | Number of cakes | Flour required (in g) |
Fat required (in g) |
| I II |
x y |
200 x 100y |
25x 50y |
| Total | x + y | 200x + 100y | 25x + 50y |
| Available Quantity | 5000 | 1000 |
Our problem is to maximize, Z = x + y ...(i)
Subject to constraints are 200x + 100y ≤ 5000
or
2x + y ≤ 50 ...(ii)
25x + 50y ≤ 1000
or x + 2y ≤ 40 ...(iii)
and x, y ≥ 0 ...(iv)
Firstly, draw the graph of the lines
2x + y = 50
| x | 0 | 25 |
| y | 50 | 0 |
Putting (0, 0) in the inequality 2x + y ≤ 50, we have
2 × 0 + 0 ≤ 50
⇒ 0 ≤ 50 (which is true)
So, the half plane is towards the origin.
Secondly, draw the graph of the line x + 2y = 40
| x | 0 | 40 |
| y | 20 | 0 |
Putting (0, 0) in the inequality x + 2y ≤ 40, we have 0 + 2 × 0 ≤ 40
⇒ 0 ≤ 40 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.

On solving equations 2x + y = 50 and x + 2y = 40, we get B(20, 10)
∴ Feasible region is OABCO.
The corner points of the feasible region are O(0, 0), A(25, 0), B(20, 10) and C(0, 20). The values of Z at these points are as follows :
| Corner Point | Z = x + y |
| O(0, 0) | 0 |
| A(25,0) | 25 |
| B(20,10) | $$30\xrightarrow{}\text{Maximum}$$ |
| C(0, 20) | 20 |
Thus, the maximum number of cakes that can be made is 30 i.e., 20 of one kind and 10 of the other kind.
3. A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making, while a cricket bat takes 3 hours of machine time of 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made, if the factory is to work at full capacity?
(ii) If the profits on a racket and on a bat is ₹ 20 and ₹ 10 respectively, find the maximum profit of the factory when it works at full capacity.
Sol. Let the number of rackets and the number of cricket bats to be made in a day be x and y respectively.
Construct the following table :
| Item | Number | Machine time (in hour) |
Craftsman's time (in hour) |
Profit (in ₹) |
| Tennis rackets Cricket bats |
x y |
1.5x 3y |
3x 1y |
20x 10y |
| Total | x + y | 1.5x + 3y | 3x + y | 20x + 10y |
| Availability | 42 | 24 |
The machine time is not available for more than 42 hours.
∴ 1.5x + 3y ≤ 42
The craftsman's time is not available for more than 24 hours.
∴ 3x + y ≤ 24
The profit on rackets is ₹ 20 and on bats is ₹ 10.
∴ Maximize Z = 20x + 10y ...(i)
Subject to constraints 1.5x + 3y ≤ 42 ...(ii)
3x + y ≤ 24 ...(iii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
1.5x + 3y = 42
| x | 0 | 28 |
| y | 14 | 0 |
Putting (0, 0) in the inequality 1.5x + 3y ≤ 42, we have
1.5 × 0 + 3 × 0 ≤ 42
⇒ 0 ≤ 42 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line
3x + y = 24
| x | 0 | 8 |
| y | 24 | 0 |
Putting (0, 0) in the inequality 3x + y ≤ 24, we have
3 × 0 + 0 ≤ 24
⇒ 0 ≤ 24 (which is true)
So, the half plane is towards the origin.
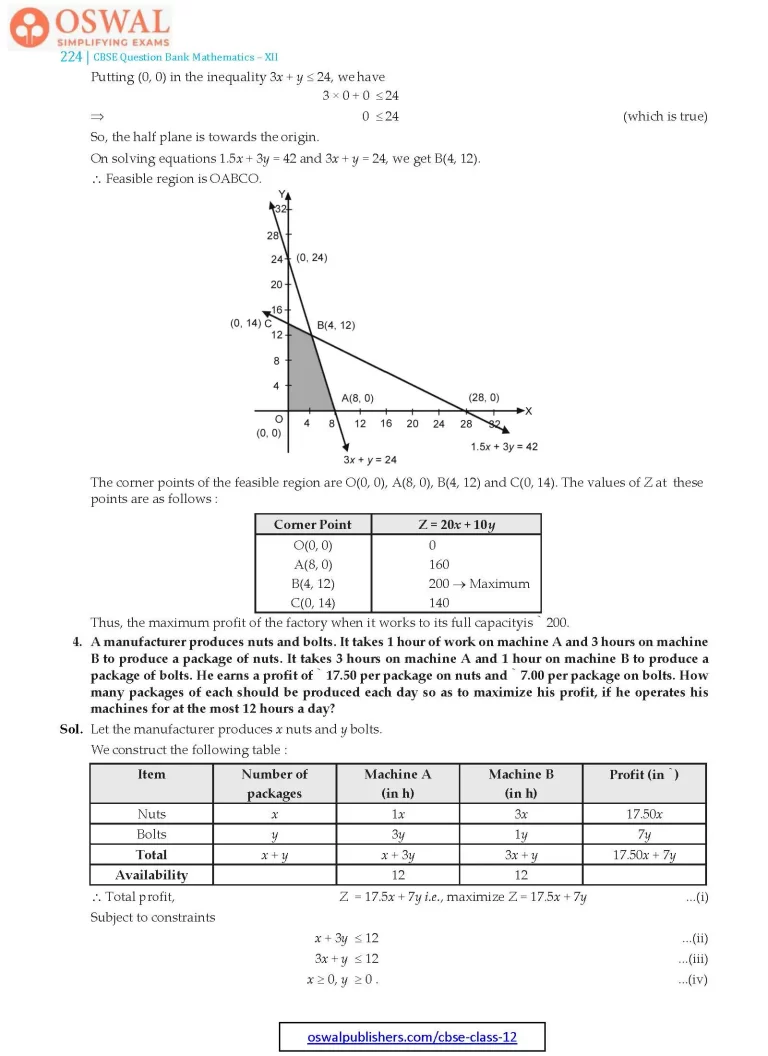
On solving equations 1.5x + 3y = 42 and 3x + y = 24, we get B(4, 12).
∴ Feasible region is OABCO.

The corner points of the feasible region are O(0, 0), A(8, 0), B(4, 12) and C(0, 14). The values of Z at these points are as follows :
| Corner Point | Z = 20x + 10y |
| O(0, 0) | 0 |
| A(8, 0) | 160 |
| B(4, 12) | $$200\xrightarrow{}\text{Maximum}$$ |
| C(0, 14) | 140 |
Thus, the maximum profit of the factory when it works to its full capacityis ₹200.
4. A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 17.50 per package on nuts and ₹ 7.00 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 12 hours a day?
Sol. Let the manufacturer produces x nuts and y bolts.
We construct the following table :
| Item | Number of packages | Machine A (in h) | Machine B (in h) | Profit (in ₹) |
| Nuts | x | 1x | 3x | 17.50x |
| Bolts | y | 3y | 1y | 7y |
| Total | x + y | x + 3y | 3x + y | 17.50x + 7y |
| Availability | 12 | 12 |
∴ Total profit, Z = 17.5x + 7y i.e., maximize Z = 17.5x + 7y ...(i)
Subject to constraints
x + 3y ≤ 12 ...(ii)
3x + y ≤ 12 ...(iii)
x ≥ 0, y ≥ 0 . ...(iv)
Firstly, draw the graph of the lines
x + 3y = 12
| x | 0 | 12 |
| y | 4 | 0 |
Putting (0, 0) in the inequality x + 3y ≤ 12, we have
0 + 3 × 0 ≤ 12
⇒ 0 ≤ 12 (which is true)
So, the half plane is towards the origin.
Since x, y ≥ 0
Secondly, draw the graph of the line
3x + y = 12
| x | 4 | 0 |
| y | 0 | 12 |
Putting (0, 0) in the inequality 3x + y ≤ 12, we have
3 × 0 + 0 ≤ 12
⇒ 0 ≤ 12 (which is true)
So, the half plane is towards the origin.
On solving equations
x + 3y = 12 and 3x + y = 12,
we get B(3, 3).
∴ Feasible region is OABCO.

The corner points of the feasible region are O(0, 0), A(4, 0), B(3, 3) and C(0, 4). The values of Z at these points are as follows :
| Corner Point | Z = 17.5x + 7y |
| O(0, 0) | 0 |
| A(4, 0) | 70 |
| B(3, 3) | $$73.50\xrightarrow{}\text{Maximum}$$ |
| C(0, 4) | 28 |
The maximum value of Z is ₹ 73.50 at (3, 3).
Thus, 3 packages of nuts and 3 packages of bolts should be produced each day to get the maximum profit ₹ 73.50.
5. A factory manufactures two types of screws A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell of package of screws A at a profit of ₹7 and screws B at a profit of ₹10. Assuming that he can sell all the screws he manufactured, how many packages of each type should be factory owner produced in a day in order to maximize his profit? Determine the maximum profit?
Sol. Let the manufacturer produces x package of screws A and y package of screws B.
We construct the following table :
| Type of screws | Number of packages | Time on automatic machine (in min) | Time on hand machine (in min) | Profit (in ₹) |
| A B |
x y |
4x 6y |
6x 3y |
7x 10y |
| Total | x + y | 4x + 6y | 6x + 3y | 7x + 10y |
| Availability | 4 × 60 = 240 | 4 × 60 = 240 |
The profits on a package of screws A is ₹7 and on the package of screws B is ₹ 10.
Maximize Z = 7x + 10y ...(i)
Subject to constraints
4x + 6y ≤ 240
or
2x + 3y ≤ 120 ...(ii)
6x + 3y ≤ 240
or
2x + y ≤ 80 ...(iii)
and x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
2x + 3y = 120
| x | 0 | 60 |
| y | 40 | 0 |
Putting (0, 0) in the inequality 2x + 3y ≤ 120, we have
2 × 0 + 3 × 0 ≤ 120
⇒ 0 ≤ 120 (which is true)
So, the half plane is towards the origin.
Secondly, draw the graph of the line 2x + y = 80
| x | 40 | 0 |
| y | 0 | 80 |
Putting (0, 0) in the inequality 2x + y ≤ 80, we have
2 × 0 + 0 ≤ 80
⇒ 0 ≤ 80 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
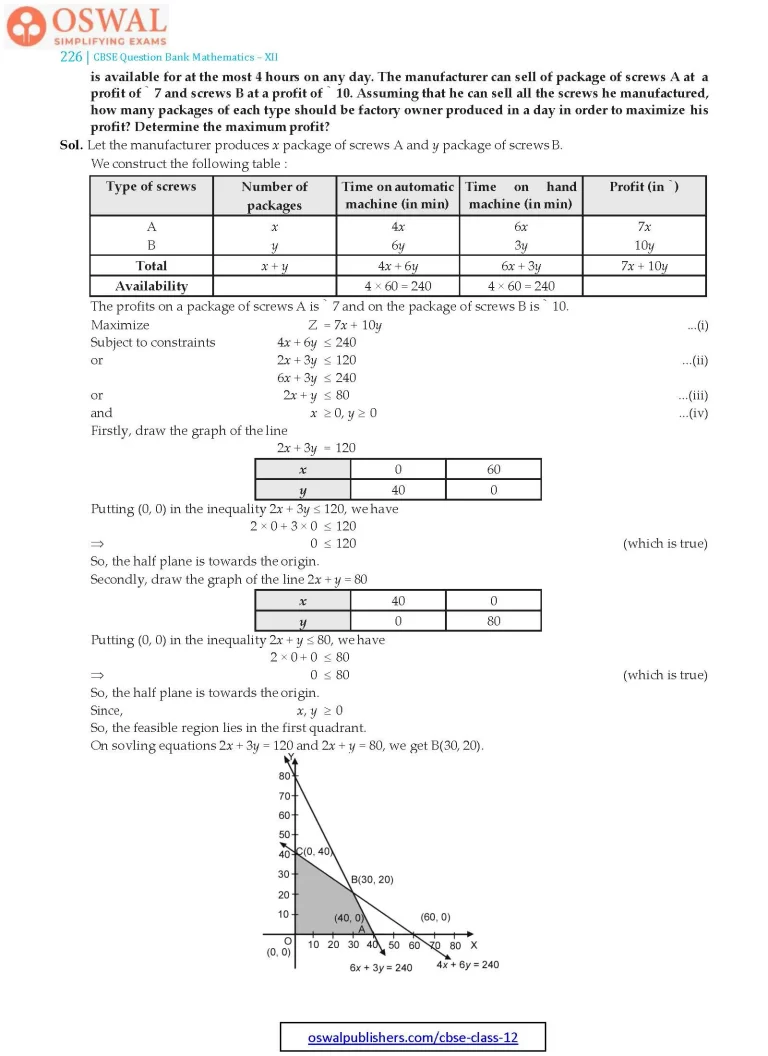
On sovling equations 2x + 3y = 120 and 2x + y = 80, we get B(30, 20).

∴ Feasible region is OABCO.
The corner points of the feasible region are O(0, 0), A(40, 0), B(30, 20) and C(0, 40). The values of Z at these points are as follows :
| Corner Point | Z = 7x + 10y |
| O(0, 0) | 0 |
| A(40, 0) | 280 |
| B(30, 20) | $$410\xrightarrow{}\text{Maximum}$$ |
| C(0, 40) | 400 |
The maximum value of Z is ₹ 410 at B(30, 20).
Thus, the factory should produce 30 package of screws A and 20 packages of screws B to get the maximum profit of ₹ 410.
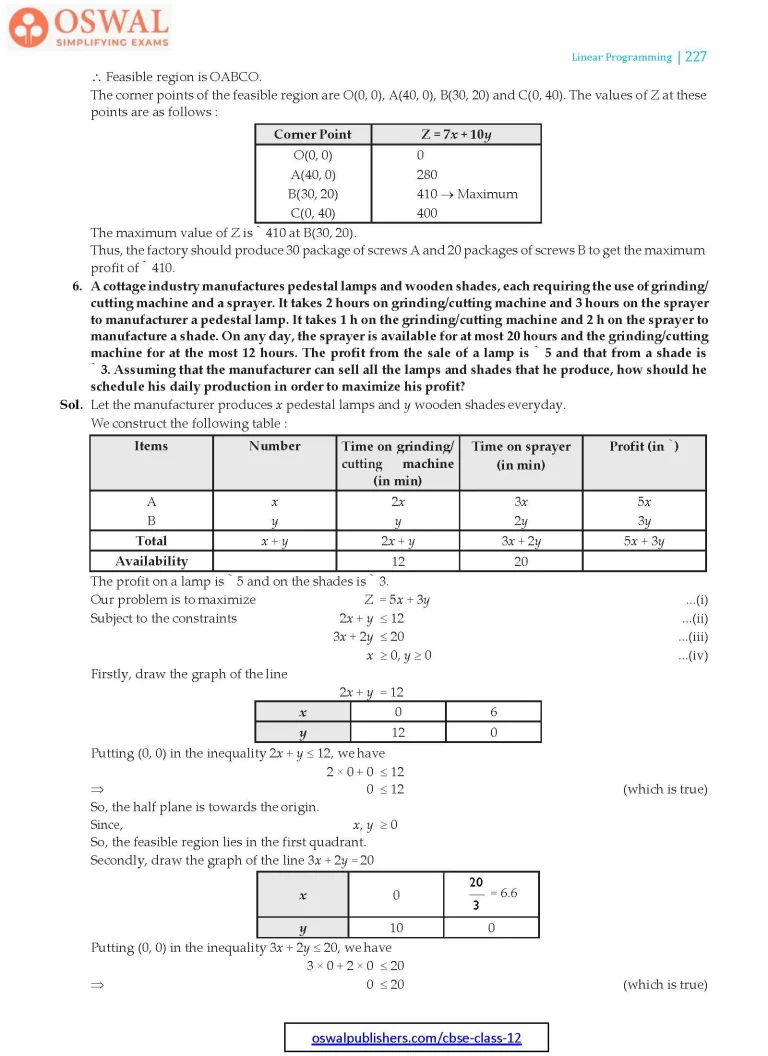
6. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacturer a pedestal lamp. It takes 1 h on the grinding/cutting machine and 2 h on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is ₹ 5 and that from a shade is ₹ 3. Assuming that the manufacturer can sell all the lamps and shades that he produce, how should he schedule his daily production in order to maximize his profit?
Sol. Let the manufacturer produces x pedestal lamps and y wooden shades everyday.
We construct the following table :
| Items | Number | Time on grinding/ cutting machine (in min) | Time on sprayer (in min) | Profit (in ₹) |
| A B |
x y |
2x y |
3x 2y |
5x 3y |
| Total | x + y | 2x + y | 3x + 2y | 5x + 3y |
| Availability | 12 | 20 |
The profit on a lamp is ₹ 5 and on the shades is ₹ 3.
Our problem is to maximize
Z = 5x + 3y ...(i)
Subject to the constraints
2x + y ≤ 12 ...(ii)
3x + 2y ≤ 20 ...(iii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
2x + y = 12
| X | 0 | 6 |
| Y | 12 | 0 |
Putting (0, 0) in the inequality 2x + y ≤ 12, we have
2 × 0 + 0 ≤ 12
⇒ 0 ≤ 12 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line 3x + 2y = 20
| X | 0 | $$\frac{20}{3}$$ =6.6 |
| Y | 10 | 0 |
Putting (0, 0) in the inequality 3x + 2y ≤ 20, we have
3 × 0 + 2 × 0 ≤ 20
⇒ 0 ≤ 20 (which is true)
So, the half plane is towards the origin.
On solving equations 2x + y = 12 and 3x + 2y = 20, we get B(4, 4).
∴ Feasible region is OABCO.
The corner points of the feasible region are O(0, 0), A(6, 0), B(4, 4) and C(0, 10). The values of Z at these points are as follows :

| Corner Point | Z = 5x + 3y |
| O(0, 0) | 0 |
| A(6, 0) | 30 |
| B(4, 4) | 32 → Maximum |
| C(0, 10) | 30 |
The maximum value of Z is ₹32 at B(4, 4).
Thus, the manufacturer should produce 4 pedestal lamps and 4 wooden shades to maximize his profits.
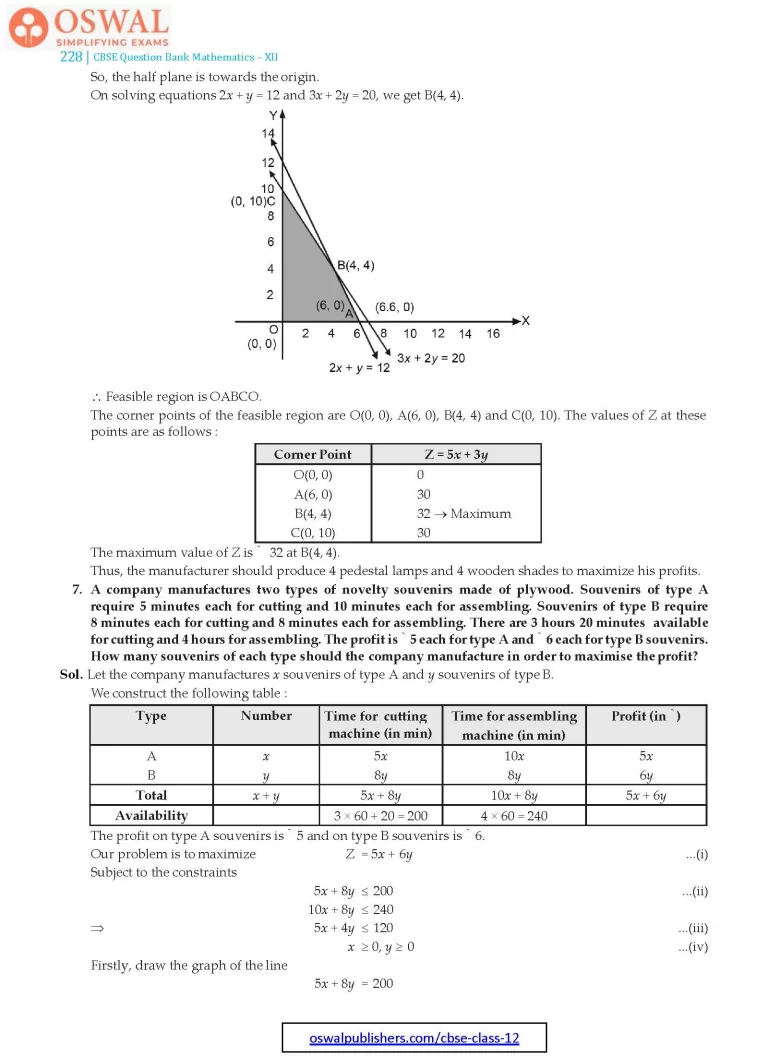
7. A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is ₹ 5 each for type A and ₹6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit?
Sol. Let the company manufactures x souvenirs of type A and y souvenirs of type B.
We construct the following table :
| Type | Number | Time for cutting machine (in min) | Time for assembling machine (in min) | Profit (in ₹) |
| A B |
x y |
5x 8y |
10x 8y |
5x 6y |
| Total | x + y | 5x + 8y | 10x + 8y | 5x + 6y |
| Availability | 3 × 60 + 20 = 200 | 4 × 60 = 240 |
The profit on type A souvenirs is ₹ 5 and on type B souvenirs is ₹6.
Our problem is to maximize
Z = 5x + 6y ...(i)
Subject to the constraints
5x + 8y ≤ 200 ...(ii)
10x + 8y ≤ 240
⇒ 5x + 4y ≤ 120 ...(iii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
5x + 8y = 200
| x | 0 | 40 |
| y | 25 | 0 |
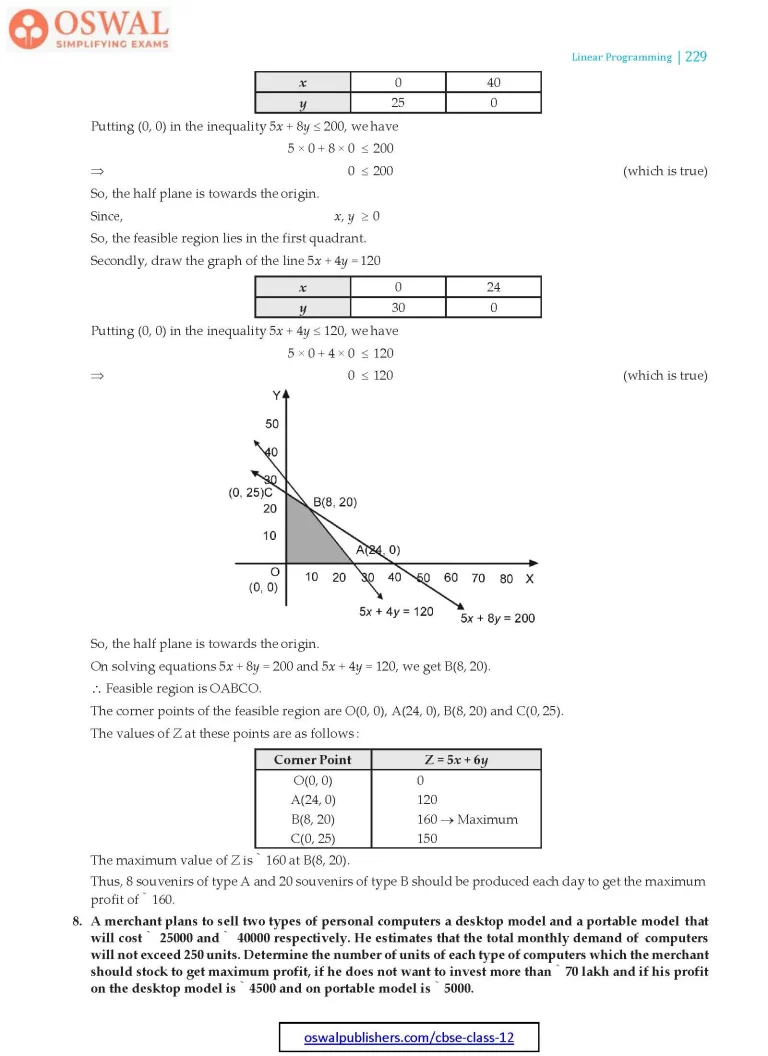
Putting (0, 0) in the inequality 5x + 8y ≤ 200, we have
5 × 0 + 8 × 0 ≤ 200
⇒ 0 ≤ 200 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line 5x + 4y = 120
| x | 0 | 24 |
| y | 30 | 0 |
Putting (0, 0) in the inequality 5x + 4y ≤ 120, we have
5 × 0 + 4 × 0 ≤ 120
⇒ 0 ≤ 120 (which is true)

So, the half plane is towards the origin.
On solving equations 5x + 8y = 200 and 5x + 4y = 120, we get B(8, 20).
∴ Feasible region is OABCO.
The corner points of the feasible region are O(0, 0), A(24, 0), B(8, 20) and C(0, 25).
The values of Z at these points are as follows :
| Corner Point | Z = 5x + 6y |
| O(0, 0) | 0 |
| A(24, 0) | 120 |
| B(8, 20) | $$160\xrightarrow{}\text{Maximum}$$ |
| C(0, 25) | 150 |
The maximum value of Z is ₹160 at B(8, 20).
Thus, 8 souvenirs of type A and 20 souvenirs of type B should be produced each day to get the maximum profit of ₹ 160.
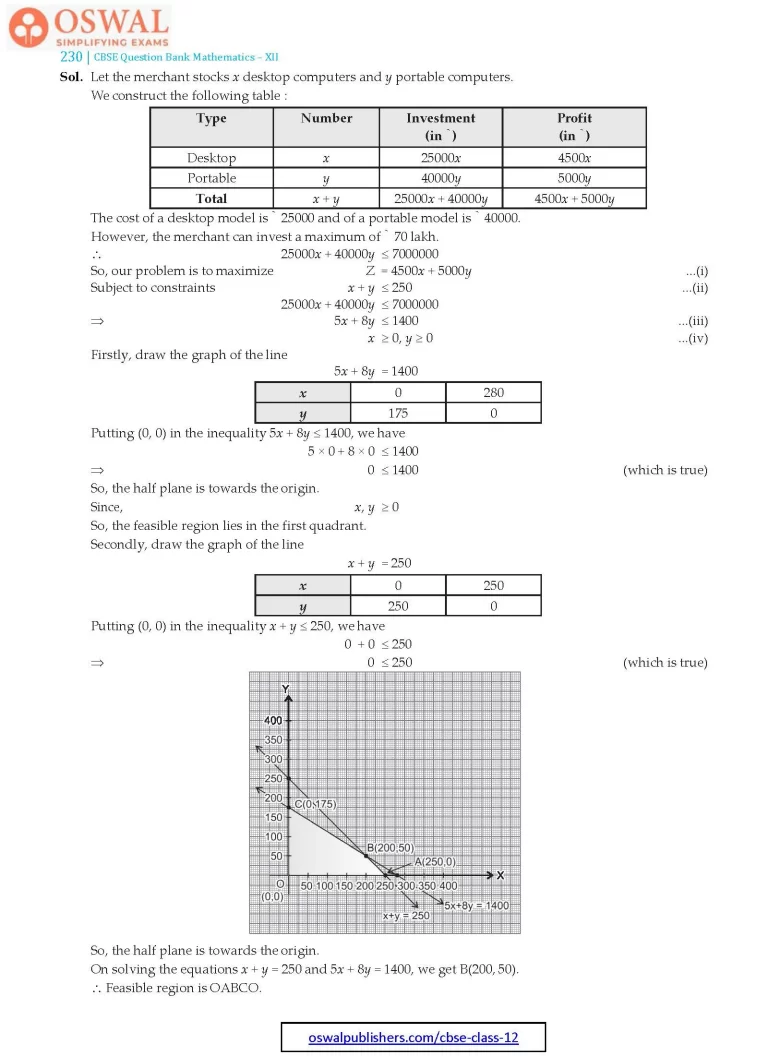
8. A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost ₹ 25000 and ₹ 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit, if he does not want to invest more than ₹ 70 lakh and if his profit on the desktop model is ₹ 4500 and on portable model is ₹ 5000.
Sol. Let the merchant stocks x desktop computers and y portable computers.
We construct the following table :
| Type | Number | Investment (in ₹) |
Profit (in ₹) |
| Desktop | x | 25000x | 4500x |
| Portable | y | 40000y | 5000y |
| Total | x + y | 25000x + 40000y | 4500x + 5000y |
The cost of a desktop model is ₹ 25000 and of a portable model is ₹40000.
However, the merchant can invest a maximum of ₹70 lakh.
∴ 25000x + 40000y ≤ 7000000
So, our problem is to maximize
Z = 4500x + 5000y ...(i)
Subject to constraints
x + y ≤ 250 ...(ii)
25000x + 40000y ≤ 7000000
⇒ 5x + 8y ≤ 1400 ...(iii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
5x + 8y = 1400
| x | 0 | 280 |
| y | 175 | 0 |
Putting (0, 0) in the inequality 5x + 8y ≤ 1400, we have
5 × 0 + 8 × 0 ≤ 1400
⇒ 0 ≤ 1400 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line
x + y = 250
| x | 0 | 250 |
| y | 250 | 0 |
Putting (0, 0) in the inequality x + y ≤ 250, we have
0 + 0 ≤ 250
⇒ 0 ≤ 250 (which is true)

So, the half plane is towards the origin.
On solving the equations x + y = 250 and 5x + 8y = 1400, we get B(200, 50).
∴ Feasible region is OABCO.
The corner points of the feasible region are O(0, 0), A(250, 0), B(200, 50) and C(0, 175). The values of Z at these points are as follows :
| Corner Point | Z = 5x + 6y |
| O(0, 0) | 0 |
| A(250, 0) | 11,25,0000 |
| B(200, 50) | $$11,50,000\xrightarrow{}\text{Maximum}$$ |
| C(0, 175) | 87,50,00 |
The maximum value of Z is 11,50,000 at point B(200, 50).
Thus, the merchant should stock 200 desktop models and 50 portable modesl to get the maximum profit of ₹ 11,50,000.
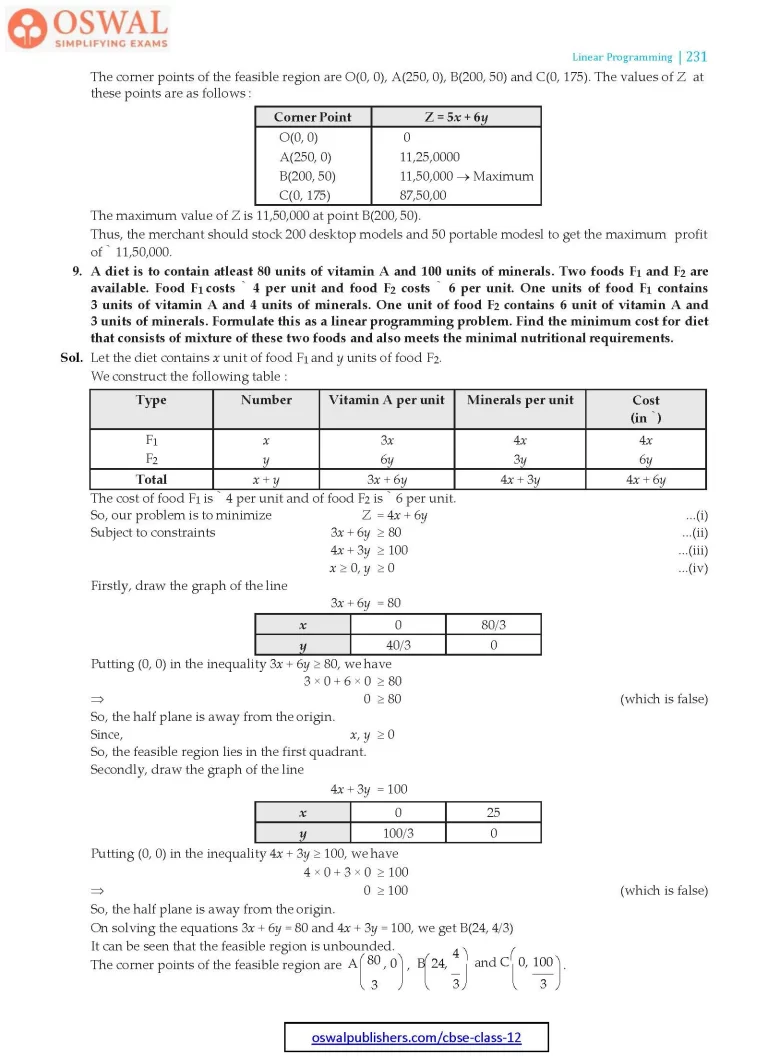
9. A diet is to contain atleast 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs ₹ 4 per unit and food F2 costs ₹6 per unit. One units of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 unit of vitamin A and
3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
Sol. Let the diet contains x unit of food F1 and y units of food F2.
We construct the following table :
| Type | Number | Vitamin A per unit | Minerals per unit | Cost (in ₹) |
| F1 F2 |
x y |
3x 6y |
4x 3y |
4x 6y |
| Total | x + y | 3x + 6y | 4x + 3y | 4x + 6y |
The cost of food F1 is ₹ 4 per unit and of food F2 is ₹6 per unit.
So, our problem is to minimize
Z = 4x + 6y ...(i)
Subject to constraints
3x + 6y ≥ 80 ...(ii)
4x + 3y ≥ 100 ...(iii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
3x + 6y = 80
4x + 3y ≥ 100 ...(iii)
x ≥ 0, y ≥ 0 ...(iv)
Firstly, draw the graph of the line
3x + 6y = 80
| x | 0 | $$\frac{80}{3}$$ |
| y | $$\frac{40}{3}$$ | 0 |
Putting (0, 0) in the inequality 3x + 6y ≥ 80, we have
3 × 0 + 6 × 0 ≥ 80
⇒ 0 ≥ 80 (which is false)
So, the half plane is away from the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line
4x + 3y = 100
| x | 0 | 25 |
| y | $$\frac{100}{3}$$ | 0 |
Putting (0, 0) in the inequality 4x + 3y ≥ 100, we have
4 × 0 + 3 × 0 ≥ 100
⇒ 0 ≥ 100 (which is false)
So, the half plane is away from the origin.
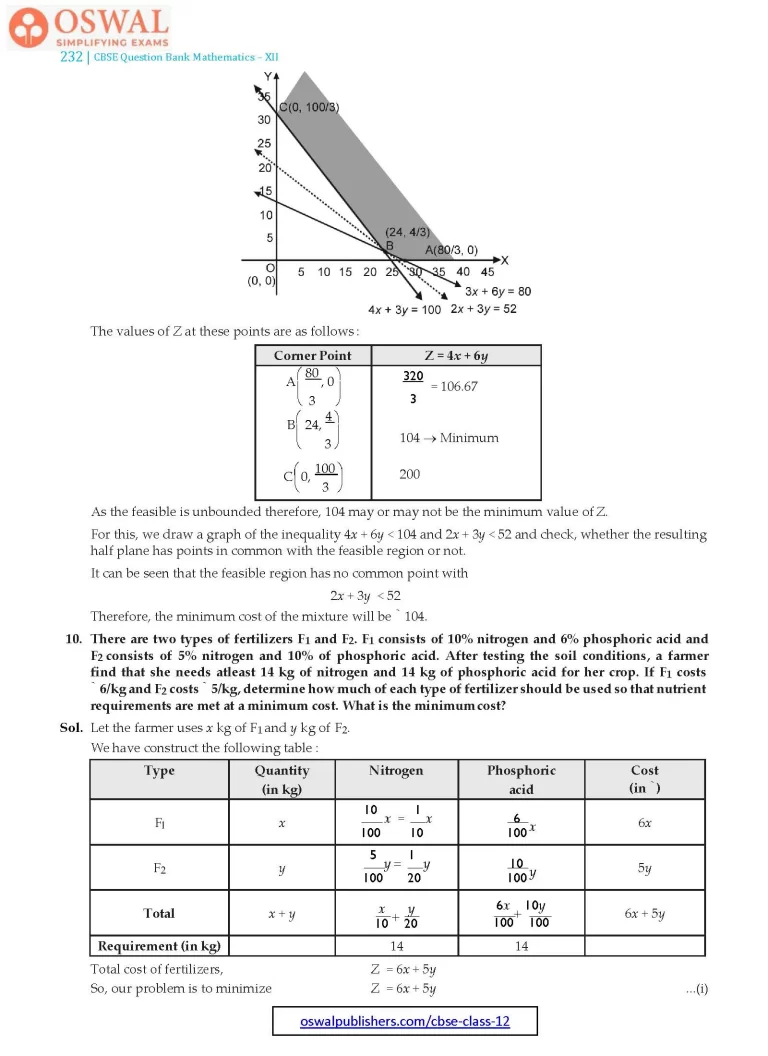
On solving the equations 3x + 6y = 80 and 4x + 3y = 100, we get B(24, 4/3)
It can be seen that the feasible region is unbounded.
The corner points of the feasible region are
$$\text{A}\bigg(\frac{80}{3},0\bigg),\text{B}\bigg(24,\frac{4}{3}\bigg)\\\text{and}\space\text{C}\bigg(0,\frac{100}{3}\bigg).$$

The values of Z at these points are as follows :
| Corner Point | Z = 4x + 6y |
| $$\text{A}\bigg(\frac{80}{3},0\bigg)$$ | $$\frac{320}{3} = 106.67$$ |
| $$\text{B}\bigg(24,\frac{4}{3}\bigg)$$ | $$104\xrightarrow{}\text{Minimum}$$ |
| $$\text{C}\bigg(0,\frac{100}{3}\bigg)$$ | 200 |
As the feasible is unbounded therefore, 104 may or may not be the minimum value of Z.
For this, we draw a graph of the inequality 4x + 6y < 104 and 2x + 3y < 52 and check, whether the resulting half plane has points in common with the feasible region or not.
It can be seen that the feasible region has no common point with
2x + 3y < 52
Therefore, the minimum cost of the mixture will be ₹ 104.
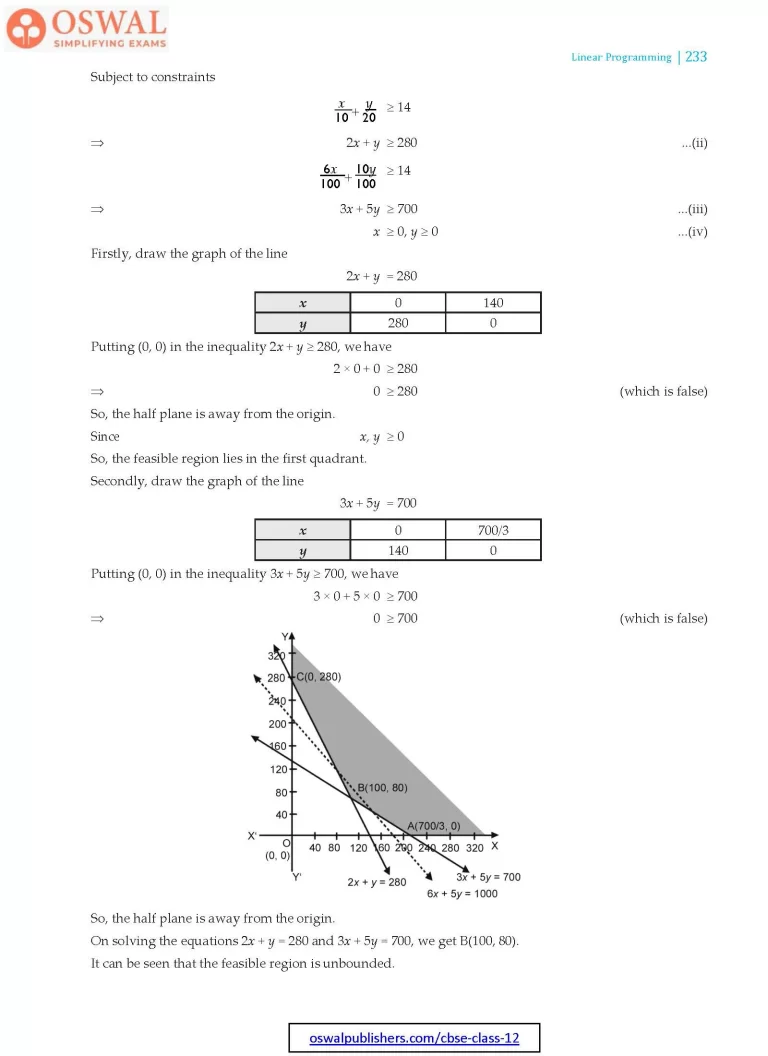
10. There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% of phosphoric acid. After testing the soil conditions, a farmer find that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs
₹ 6/kg and F2 costs ₹ 5/kg, determine how much of each type of fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
Sol. Let the farmer uses x kg of F1 and y kg of F2.
We have construct the following table :
| Type | Quantity (in kg) |
Nitrogen | Phosphoric acid | Cost (in ₹) |
| F1 | x | $$\frac{10}{100}x = \frac{1}{10}x$$ | $$\frac{6}{100}x$$ | 6x |
| F2 | y | $$\frac{5}{100}y = \frac{1}{20}y$$ | $$\frac{10}{100}y$$ | 5y |
| Total | x + y | $$\frac{x}{10}+\frac{y}{20}$$ | $$\frac{6x}{100} + \frac{10y}{100} $$ | 6x + 5y |
| Requirement (in kg) | 14 | 14 |
Total cost of fertilizers,
Z = 6x + 5y
So, our problem is to minimize
Z = 6x + 5y ...(i)
Subject to constraints
$$\frac{x}{10}+\frac{y}{20}\geq14\\\Rarr\space 2x+y\geq280\space\text{...(ii)}\\\frac{6x}{100} + \frac{10y}{100}\geq 14\\\Rarr\space 3x+5y\geq700\space\text{...(iii)}\\x\geq0, y\geq0\space\text{...(iv)}$$
Firstly, draw the graph of the line
2x + y = 280
| x | 0 | 140 |
| y | 280 | 0 |
Putting (0, 0) in the inequality 2x + y ≥ 280, we have
2 × 0 + 0 ≥ 280
$$\Rarr\space 0\geq280\space\text{(which is false)}$$
So, the half plane is away from the origin.
Since x, y ≥ 0
So, the feasible region lies in the first quadrant.
Secondly, draw the graph of the line
3x + 5y = 700
| x | 0 | $$\frac{700}{3}$$ |
| y | 140 | 0 |
Putting (0, 0) in the inequality 3x + 5y ≥ 700, we have
3 × 0 + 5 × 0 ≥ 700
$$\Rarr\space 0\geq700\space\text{(which is false)}$$

So, the half plane is away from the origin.
On solving the equations 2x + y = 280 and 3x + 5y = 700, we get B(100, 80).
It can be seen that the feasible region is unbounded.
The corner points of the feasible region are
$$A\bigg(\frac{700}{3},0\bigg),\space\text{B(100, 80) and C(0, 280).}$$
The value of Z at these points are as follows :
| Corner Point | Z = 6x + 5y |
| $$A\bigg(\frac{700}{3},0\bigg)$$ | 1400 |
| B(100, 80) | $$\text{1000}\xrightarrow{}\text{Minimum}$$ |
| C(0, 280) | 1400 |
As the feasible region is unbounded theefore, 1000 may or may not be the minimum
value of Z. For this, we draw a graph of the inequality, 6x + 5y < 1000 and check, whether the resulting half plane has points in common with the feasible region or not.
It can be seen that the feasible region has no common point with 6x + 5y < 1000.
Therefore, 100 kg of fertilizer F1 and 80 kg of fertilizer F2 should be used to minimize the cost. The minimum cost is ₹ 1000.
11. The corner points of the feasible region determined by the following system of linear inequalities :
2x + y ≤ 10, x + 3y ≤ 15, x + y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is :
(a) p = q
(b) p = 2q
(c) p = 3q
(d) q = 3p
Sol. (d) q = 3p
The maximum value of Z is unique.
It is given that the maximum value of Z occurs at two points (3, 4) and (0, 5).
Value of Z at (3, 4) = Value of Z at (0, 5).
⇒ p(3) + q(4) = p(0) + q(5)
3p + 4q = 5q
⇒ q = 3p
