NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions - Miscellaneous Exercise






Access Exercises of Class 12 Maths Chapter 2 – Inverse Trigonometric Functions
Exercise 2.1 Solutions: 14 Questions (12 Short Answers, 2 MCQs)
Exercise 2.2 Solutions: 21 Questions (18 Short Answers, 3 MCQs)
Miscellaneous Exercise Solutions: 17 Questions (14 Short Answers, 3 MCQs)
Miscellaneous Exercise
Find the value of following functions :
$$\textbf{1.\space}\textbf{cos}^{\normalsize-1}\bigg(\textbf{cos}\frac{\textbf{13}\pi}{\textbf{6}}\bigg)\textbf{.}\\\textbf{Sol.}\space\text{cos}^{\normalsize-1}\bigg(\text{cos}\frac{13\pi}{6}\bigg)\\=\text{cos}^{\normalsize-1}\bigg[\text{cos}\bigg(2\pi + \frac{\pi}{6}\bigg)\bigg];\\\text{where}\frac{\pi}{6}\epsilon\lbrack0,\pi\rbrack$$
[Hence, the given angle does not lie in the principal interval i.e., [0, π], so we convert it such that it lies in [0, π]
$$= \text{cos}^{\normalsize-1}\bigg[\text{cos}\bigg(\frac{\pi}{6}\bigg)\bigg] = \frac{\pi}{6}\\\lbrack\because\space \text{cos}(2\pi +\theta) =\text{cos}\space\theta\rbrack$$
$$\textbf{2.\space tan}^{\normalsize-1}\bigg(\textbf{tan}\frac{\textbf{7}\pi}{\textbf{6}}\bigg)\\\textbf{Sol.\space}\text{tan}^{\normalsize-1}\bigg(\text{tan}\frac{7\pi}{6}\bigg)\\=\text{tan}^{\normalsize-1}\bigg[\text{tan}\bigg(\pi + \frac{\pi}{6}\bigg)\bigg];\\\text{where}\space\frac{\pi}{6}\epsilon\bigg(-\frac{\pi}{2},\frac{\pi}{2}\bigg)\\\text{(Principal interval)}\\\therefore\space\text{tan}^{\normalsize-1}\bigg(\text{tan}\frac{7\pi}{6}\bigg)\\=\text{tan}^{\normalsize-1}\bigg[\text{tan}\frac{\pi}{6}\bigg]=\frac{\pi}{6}\\\lbrack\because\space \text{tan}(\pi +\theta) =\text{tan}\space\theta\rbrack$$
Prove the following functions :
$$\textbf{3. 2sin}^{\normalsize-1}\frac{\textbf{3}}{\textbf{5}} =\textbf{tan}^{\normalsize-1}\frac{\textbf{24}}{\textbf{7}}\textbf{.}\\\textbf{Sol.\space}\text{Given, 2 sin}^{\normalsize-1}\frac{3}{5} \\=\text{tan}^{\normalsize-1}\frac{24}{7}\\\text{LHS = 2 sin}^{\normalsize-1}\frac{3}{5}\\=\text{sin}^{\normalsize-1}\bigg[2×\frac{3}{5}\sqrt{1-\bigg(\frac{3}{5}\bigg)^{2}}\bigg]\\\lbrack\because\space \text{2 sin}^{\normalsize-1}y = \\\text{sin}^{\normalsize-1}(2y\sqrt{1-y^{2}})\rbrack\\=\text{sin}^{\normalsize-1}\bigg[2×\frac{3}{6}×\frac{4}{5}\bigg]$$
$$=\space\text{sin}^{\normalsize-1}\bigg(\frac{24}{25}\bigg)\\=\text{tan}^{\normalsize-1}\begin{bmatrix}\frac{\frac{24}{25}}{\sqrt{1 - \bigg(\frac{24}{25}\bigg)^{2}}}\end{bmatrix}\\\bigg(\because\space\text{sin}^{\normalsize-1} y =\text{tan}^{\normalsize-1}\frac{y}{\sqrt{1-y^{2}}}\bigg)$$
$$=\text{tan}^{\normalsize-1}\begin{bmatrix}\frac{\frac{24}{25}}{\sqrt{1 -\frac{576}{625}}}\end{bmatrix}\\=\text{tan}^{\normalsize-1}\bigg[\frac{24}{25}×\frac{25}{7}\bigg]\\=\text{tan}^{\normalsize-1}\bigg[\frac{24}{7}\bigg]=\text{RHS.}\\\textbf{Hence proved.}$$
$$\textbf{4. sin}^{\normalsize-1}\frac{\textbf{8}}{\textbf{17}} \textbf{+}\textbf{sin}^{\normalsize-1}\frac{\textbf{3}}{\textbf{5}}\\\textbf{= tan}^{\normalsize-1}\frac{\textbf{77}}{\textbf{36}}\\\textbf{Sol.\space}\text{Given, sin}^{\normalsize-1}\frac{8}{17} + \text{sin}^{\normalsize-1}\frac{3}{5}\\=\text{tan}^{\normalsize-1}\frac{77}{36}\\\text{LHS} =\\ \text{sin}^{\normalsize-1}\bigg(\frac{8}{17}\bigg) + \text{sin}^{\normalsize-1}\bigg(\frac{3}{5}\bigg)\\=\text{sin}^{\normalsize-1}\begin{bmatrix}\frac{8}{17}\sqrt{1 -\bigg(\frac{3}{5}\bigg)^{2}} +\\ \frac{3}{5}\sqrt{1 -\bigg(\frac{8}{17}\bigg)^{2}}\end{bmatrix}$$
$$\lbrack\because\space\text{sin}^{\normalsize-1}x + \text{sin}^{\normalsize-1}y\\\text{sin}^{\normalsize-1}(x\sqrt{1-y^{2}}+y\sqrt{1-x^{2}})\rbrack\\=\text{sin}^{\normalsize-1}\bigg(\frac{8}{17}×\frac{4}{5} + \frac{3}{5}×\frac{15}{17}\bigg)\\=\text{sin}^{\normalsize-1}\bigg(\frac{77}{85}\bigg)\\=\text{tan}^{\normalsize-1}\begin{bmatrix}\frac{\frac{77}{85}}{\sqrt{1-\bigg(\frac{77}{85}\bigg)^{2}}}\end{bmatrix}\\\bigg(\because\space\text{sin}^{-1}x = \text{tan}^{\normalsize-1}\frac{x}{\sqrt{1 - x^{2}}}\bigg)\\=\text{tan}^{\normalsize-1}\bigg[\frac{77}{85}×\frac{85}{36}\bigg]$$
$$=\text{tan}^{\normalsize-1}\frac{77}{36}=\text{RHS.}\\\textbf{Hence proved.}$$
$$\textbf{5.\space cos}^{\normalsize-1}\frac{\textbf{4}}{\textbf{5}} \textbf{+}\textbf{cos}^{\normalsize-1}\frac{\textbf{12}}{\textbf{13}}\\=\textbf{cos}^{\normalsize-1}\frac{\textbf{33}}{\textbf{65}}\textbf{.}\\\textbf{Sol.\space}\text{Given,}\\\text{cos}^{\normalsize-1}\frac{4}{5}+\text{cos}^{\normalsize-1}\frac{12}{13}\\=\text{cos}^{\normalsize-1}\frac{33}{65}\\\text{LHS} = \\\text{cos}^{\normalsize-1}\bigg(\frac{4}{5}\bigg) + \text{cos}^{\normalsize-1}\bigg(\frac{12}{13}\bigg)\\=\text{cos}^{\normalsize-1}\\\bigg(\frac{4}{5}.\frac{12}{13}-\sqrt{1-\bigg(\frac{4}{5}\bigg)^{2}}\sqrt{1-\bigg(\frac{12}{13}\bigg)^{2}}\bigg)$$
$$\lbrack\because\space\text{cos}^{\normalsize-1}x + \text{cos}^{-1}y\\=\text{cos}^{-1}(xy -\sqrt{1-x^{2}}\sqrt{1 - y^{2}})\rbrack\\=\text{cos}^{\normalsize-1}\bigg(\frac{48}{65} -\sqrt{\bigg(\frac{3}{5}\bigg)^{2}}\sqrt{\bigg(\frac{5}{13}\bigg)^{2}}\bigg)\\=\text{cos}^{\normalsize-1}\bigg(\frac{48}{65} - \frac{3}{5}×\frac{5}{13}\bigg)\\=\text{cos}^{\normalsize-1}\bigg(\frac{48}{65} -\frac{3}{13}\bigg)\\=\text{cos}^{\normalsize-1}\bigg(\frac{33}{65}\bigg)\\=\text{RHS.}\space\textbf{Hence proved.}$$
$$\textbf{6. cos}^{\normalsize-1}\frac{\textbf{12}}{\textbf{13}} \textbf{+}\textbf{sin}^{\normalsize-1}\frac{\textbf{3}}{\textbf{5}}\\=\textbf{sin}^{\normalsize-1}\frac{\textbf{56}}{\textbf{65}}\\\textbf{Sol.\space}\text{Given,}\\\text{cos}^{\normalsize-1}\frac{12}{13} + \text{sin}^{\normalsize-1}\frac{3}{5}\\=\text{sin}^{\normalsize-1}\frac{56}{65}\\\text{Let\space}\text{cos}^{\normalsize-1}\frac{12}{13} = \theta\\\Rarr\space\text{cos}\space\theta =\frac{12}{13}\\\therefore\space\text{sin}\space\theta =\sqrt{1 - \bigg(\frac{12}{13}\bigg)^{2}}$$
$$\lbrack\because\space\text{sin}\space\theta =\sqrt{1 - cos^{2}}\theta\rbrack\\\Rarr\space\text{sin}\space\theta=\sqrt{\frac{25}{169}}=\frac{5}{13}\\\Rarr\space\theta = \text{sin}^{\normalsize-1}\frac{5}{13}\\\text{Now,\space LHS = cos}^{\normalsize-1}\frac{12}{13} +\text{sin}^{\normalsize-1}\frac{3}{5}\\=\text{sin}^{\normalsize-1}\frac{5}{13} + \text{sin}^{\normalsize-1}\frac{3}{5}\\=\text{sin}^{\normalsize-1}\bigg(\frac{5}{13}\sqrt{1 -\bigg(\frac{3}{5}\bigg)^{2}} + \\\frac{3}{5}\sqrt{1 -\bigg(\frac{5}{13}\bigg)^{2}}\bigg)$$
$$\lbrack\because\space\text{sin}^{\normalsize-1}x + \text{sin}^{\normalsize-1}y\\ = \text{sin}^{\normalsize-1}(x\sqrt{1 - y^{2}} + y\sqrt{1- x^{2}})\rbrack\\=\text{sin}^{\normalsize-1}\bigg(\frac{5}{13}\sqrt{\frac{16}{25}} + \frac{3}{5}\sqrt{\frac{144}{169}}\bigg)\\=\text{sin}^{\normalsize-1}\bigg(\frac{5}{13}×\frac{4}{5} + \frac{3}{5}×\frac{12}{13}\bigg)\\=\text{sin}^{\normalsize-1}\bigg(\frac{56}{65}\bigg)=\text{RHS}\\\textbf{Hence proved.}$$
$$\textbf{7.\space}\textbf{tan}^{\normalsize-1}\frac{\textbf{63}}{\textbf{16}} =\\\textbf{sin}^{\normalsize-1}\frac{\textbf{5}}{\textbf{13}} \textbf{+}\textbf{cos}^{\normalsize-1}\frac{\textbf{3}}{\textbf{5}}.\\\textbf{Sol.\space}\text{Given, tan}^{\normalsize-1}\frac{63}{16}\\=\text{sin}^{\normalsize-1}\frac{5}{13} + \text{cos}^{\normalsize-1}\frac{3}{5}\\\text{RHS = sin}^{\normalsize-1}\frac{5}{13} + \text{cos}^{\normalsize-1}\frac{3}{5}\\\text{Let}\space\text{sin}^{\normalsize-1}\bigg(\frac{5}{13}\bigg) = x\\\Rarr\space \text{sin x =}\frac{5}{13}$$
∵ 1 – sin2x = cos2 x
$$\Rarr\space1 -\bigg(\frac{5}{13}\bigg)^{2} =\text{cos}^{2}x\\\Rarr\space \frac{169-25}{169}=\text{cos}^{2}x\\\Rarr\space \frac{144}{169} = \text{cos}^{2}x\\\Rarr\space \frac{12}{13}=\text{cos x}\\\therefore\space\text{tan x} =\frac{\text{sin x}}{\text{cos x}}\\\Rarr\space \text{tan}\space x =\frac{\frac{5}{13}}{\frac{12}{13}}=\frac{5}{12}\\\Rarr\space \text{x = tan}^{\normalsize-1}\frac{5}{12}$$
$$\text{Let\space cos}^{\normalsize-1}\frac{3}{5} = y\\\Rarr\space\text{cos y} =\frac{3}{5}\\\because\space\text{1 - cos}^{2}y = \text{sin}^{2}y\\\Rarr\space 1-\bigg(\frac{3}{5}\bigg)^{2} - \text{sin}^{2}y\\\Rarr\space\frac{25-9}{25} = \text{sin}^{2}y\\\Rarr\space\frac{16}{25} =\text{sin}^{2}y\\\Rarr\space \frac{4}{5} = \text{sin y}\\\text{tan y} = \frac{\text{sin y}}{\text{cos y}}$$
$$\Rarr\space\text{tan y} =\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}\\\Rarr y =\text{tan}^{\normalsize-1}\frac{4}{3}\\\therefore\space\text{Given equation becomes}\\\text{tan}^{\normalsize-1}\frac{63}{16} = x+y\\\Rarr\space \text{tan}^{\normalsize-1}\frac{63}{16} =\text{tan}^{\normalsize-1}\bigg(\frac{5}{12}\bigg) +\\ \text{tan}^{\normalsize-1}\bigg(\frac{4}{3}\bigg)\\\therefore\space\text{RHS = tan}^{\normalsize-1}\bigg(\frac{5}{12}\bigg) + \text{tan}^{\normalsize-1}\bigg(\frac{4}{3}\bigg)$$
$$= \text{tan}^{\normalsize-1}\begin{bmatrix}\frac{\frac{5}{12} + \frac{4}{3}}{1 - \frac{5}{12}×\frac{4}{3}}\end{bmatrix}\\\bigg[\because\space\text{tan}^{\normalsize-1}x + \text{tan}^{\normalsize-1}y\\=\text{tan}^{\normalsize-1}\bigg(\frac{x+y}{1-xy}\bigg)\bigg]$$
$$=\text{tan}^{\normalsize-1}\begin{bmatrix}\frac{\frac{15 +48}{12×3}}{\frac{12×3-20}{12×3}}\end{bmatrix}\\=\text{tan}^{\normalsize-1}\bigg[\frac{63}{36}×\frac{36}{36-20}\bigg]\\=\text{tan}^{\normalsize-1}\bigg[\frac{63}{16}\bigg]=\text{RHS}$$
∴ LHS = RHS Hence proved.
$$\textbf{8. tan}^{\normalsize-1}\frac{\textbf{1}}{\textbf{5}} \textbf{+}\textbf{tan}^{\normalsize-1}\frac{\textbf{1}}{\textbf{7}}\textbf{+}\\\textbf{tan}^{\normalsize-1}\frac{\textbf{1}}{\textbf{3}} \textbf{+}\textbf{tan}^{\normalsize-1}\frac{\textbf{1}}{\textbf{8}}\textbf{=}\frac{\pi}{\textbf{4}}\\\textbf{Sol.\space} \text{Given},\space\text{tan}^{-1}\frac{1}{5} + \text{tan}^{\normalsize-1}\frac{1}{7}+\\\text{tan}^{\normalsize-1}\frac{1}{3} + \text{tan}^{\normalsize-1}\frac{1}{8}=\frac{\pi}{4}\\\text{LHS}= \bigg(\text{tan}^{\normalsize-1}\frac{1}{5} + \text{tan}^{\normalsize-1}\frac{1}{7}\bigg) +\\\bigg(\text{tan}^{\normalsize-1}\frac{1}{3} + \text{tan}^{\normalsize-1}\frac{1}{8}\bigg)\\=\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\frac{1}{5} + \frac{1}{7}}{1 - \frac{1}{5}×\frac{1}{7}}\end{pmatrix} + \\\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\frac{1}{3} + \frac{1}{2}}{1 -\frac{1}{3}×\frac{1}{8}}\end{pmatrix}$$
$$\bigg[\because\space\text{tan}^{\normalsize-1}x +\text{tan}^{\normalsize-1}y =\\\text{tan}^{\normalsize-1}\bigg(\frac{x+y}{1 - xy}\bigg)\bigg]$$
$$= \text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\frac{7+5}{35}}{\frac{35-1}{35}}\end{pmatrix} + \text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\frac{8+3}{24}}{\frac{24-1}{24}}\end{pmatrix}\\=\text{tan}^{\normalsize-1}\bigg(\frac{6}{17}\bigg) + \text{tan}^{\normalsize-1}\bigg(\frac{11}{23}\bigg)\\=\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\frac{6}{17}+\frac{11}{23}}{1- \frac{6}{17}×\frac{11}{23}}\end{pmatrix}+\\\text{tan}^{\normalsize-1}\bigg(\frac{6×23 + 11×17}{17×23 - 6×11}\bigg)\\=\text{tan}^{\normalsize-1}\bigg(\frac{325}{325}\bigg)\\=\text{tan}^{\normalsize-1}1 \frac{\pi}{4}=\text{RHS.}$$
Hence proved.
Prove that :
$$\textbf{9.\space tan}^{\normalsize-1}\sqrt{\textbf{x}}\space\textbf{=}\space\\\frac{\textbf{1}}{\textbf{2}}\textbf{cos}^{\normalsize-1}\bigg(\frac{\textbf{1-x}}{\textbf{1+x}}\bigg)\textbf{,}\space \textbf{x}\epsilon\lbrack\textbf{0,1}\rbrack\\\textbf{Sol.\space}\text{Given, tan}^{\normalsize-1}\sqrt{x} \\=\frac{1}{2}\text{cos}^{\normalsize-1}\bigg(\frac{\text{1-x}}{\text{1+x}}\bigg), x\epsilon\lbrack0,1\rbrack\\\text{LHS = tan}^{\normalsize-1}\sqrt{x}\\=\frac{1}{2}×(2×\text{tan}^{\normalsize-1}\sqrt{x})\\=\frac{1}{2}×\text{cos}^{\normalsize-1}\frac{1 - (\sqrt{x})^{2}}{1 + (\sqrt{x})^{2}}\\\begin{bmatrix}\because\space 2\text{tan}^{\normalsize-1}x = \text{cos}^{\normalsize-1}\bigg(\frac{\text{1 - x}^{2}}{\text{1 + x}^{2}}\bigg)\end{bmatrix}\\=\frac{1}{2}\text{cos}^{\normalsize-1}\bigg(\frac{1-x}{1 +x}\bigg)=\text{RHS.}$$
Hence proved.
$$\textbf{10. cot}^{\normalsize-1}\bigg(\frac{\sqrt{\textbf{1 + sin x}} + \sqrt{\textbf{1 - sin x}}}{\sqrt{\textbf{1 + sin x}} - \sqrt{\textbf{1 - sin x}}}\bigg)\\=\frac{\textbf{x}}{\textbf{2}}\textbf{,}\space \textbf{x}\epsilon\bigg(0,\frac{\pi}{\textbf{4}}\bigg)$$
Sol. Given,
$$\text{cot}^{\normalsize-1}\begin{pmatrix}\frac{\sqrt{1 + sin x} + \sqrt{1 - sin x}}{\sqrt{1 + sin x} -\sqrt{1 - sin x}}\end{pmatrix}\\=\frac{x}{2}, x\epsilon\bigg(0,\frac{\pi}{4}\bigg)\\\text{LHS =}\\\text{ cot}^{\normalsize-1}\bigg(\frac{\sqrt{1 + sin x} + \sqrt{1 - sin x}}{\sqrt{1 + sin x}\space-\space\sqrt{1 - sinx}}\bigg)\\\text{...(i)}$$
Now, we can write
$$\sqrt{\text{1 + sin x}} =\\\sqrt{\text{sin}^{2}\frac{x}{2} + \text{cos}^{2}\frac{x}{2} + 2\text{sin}\frac{x}{2}\text{cos}\frac{x}{2}}\\=\sqrt{\bigg(\text{sin}\frac{x}{2} + \text{cos}\frac{x}{2}\bigg)^{2}} \\\begin{bmatrix}\because\space\text{sin}^{2}\frac{x}{2} + \text{cos}^{2}\frac{x}{2}=1\\\text{and \space sin x = 2sin}\frac{x}{2}\text{cos}\frac{x}{2}\end{bmatrix}\\\Rarr\space\sqrt{\text{1 + sinx}} \\=\text{sin}\frac{x}{2} + \text{cos}\frac{x}{2}$$
Similarly, we can get
$$\sqrt{\text{1 - sin x}} = \text{cos}\frac{x}{2} - \text{sin}\frac{x}{2}$$
On substituting above two values in Eq. (i), we get
$$\text{LHS }\\\text{= cot}^{\normalsize-1}\begin{pmatrix}\frac{\text{sin}\frac{x}{2} + \text{cos}\frac{x}{2} + \text{cos}\frac{x}{2} -\text{sin}\frac{x}{2}}{\text{sin}\frac{x}{2} + \text{cos}\frac{x}{2} + \text{sin}\frac{x}{2} -\text{cos}\frac{x}{2}}\end{pmatrix}\\=\text{cot}^{\normalsize-1}\begin{pmatrix}\frac{\text{2 cos}\frac{x}{2}}{\text{2 sin}\frac{x}{2}}\end{pmatrix}\\=\text{cot}^{\normalsize-1}\bigg(\text{cot}\frac{x}{2}\bigg)=\frac{x}{2}=\text{RHS}$$
Alternative method
$$\text{LHS} =\\ \text{cot}^{\normalsize-1}\frac{\sqrt{\text{1 + sinx}} + \sqrt{\text{1 - sin x}}}{\sqrt{\text{1 + sin x}}-\sqrt{\text{1 - sin x}}}\\=\text{cot}^{\normalsize-1}\\\begin{bmatrix}\frac{\sqrt{\text{1 + sin x}} + \sqrt{\text{1 - sin x}}}{\sqrt{\text{1 + sin x}} - \sqrt{\text{1 - sinx}}}×\\\frac{\sqrt{\text{1 + sin x}} + \sqrt{\text{1 - sin x}}}{\sqrt{\text{1 + sin x}} +\sqrt{\text{1 - sin x}}}\end{bmatrix}$$
(by rationalyzing denominator)
$$=\text{cot}^{\normalsize-1}\begin{bmatrix}\frac{(\sqrt{1 + sin \space x} + \sqrt{1 - sin x})^{2}}{(\sqrt{\text{1 + sinx}})^{2} - (\sqrt{\text{1 - sin x}})^{2}}\end{bmatrix}\\=\text{cot}^{\normalsize-1}\\\begin{bmatrix}\frac{\text{1 + sinn x +1 - sin x +2}\sqrt{\text{1 - sin}^{2}x}}{\text{1 + sin x - 1 + sin x}}\end{bmatrix}\\=\text{cot}^{\normalsize-1}\bigg[\frac{\text{2 +2 cos x}}{\text{2 sin x}}\bigg]\\\begin{bmatrix}\because\space \text{cos}^{2}x + \text{sin}^{2}x=1\\\Rarr\space\text{cos x} = \sqrt{\text{1 - sin}^{2}x}\end{bmatrix}\\=\text{cot}^{\normalsize-1}\bigg[\frac{\text{1 + cos x}}{\text{sin x}}\bigg]\\=\text{cot}^{\normalsize-1}\bigg[\frac{\text{2 cos}^{2}\space\text{x/2}}{\text{2 sin x/2 cos x/2}}\bigg]$$
$$\begin{pmatrix}\because\space \text{1 + cos x = 2 cos}^{2}\frac{x}{2}\\\text{ and sin x = 2 sin}\frac{x}{2}\text{cos}\frac{x}{2}\end{pmatrix}\\=\text{cot}^{\normalsize-1}\bigg[\text{cot}\frac{x}{2}\bigg]=\frac{x}{2} = \text{RHS}\\\textbf{Note :\space}\text{If x}\epsilon\bigg(0,\frac{\pi}{2}\bigg),\space\text{then}\\=\sqrt{\text{1 - sin x}} = \text{cos}\frac{x}{2} -\text{sin}\frac{x}{2}\\\text{and if}\space x\epsilon\bigg(\frac{\pi}{2},\pi\bigg),\text{then}\\\sqrt{\text{1 - sin x}} =\text{sin}\frac{x}{2}-\text{cos}\frac{x}{2}$$
$$\textbf{11.\space tan}^{\normalsize-1}\bigg(\frac{\sqrt{\textbf{1 + x}} \textbf{-}\sqrt{\textbf{1- x}}}{\sqrt{\textbf{1 + x}} \textbf{+} \sqrt{\textbf{1 - x}}}\bigg)\\=\frac{\pi}{\textbf{4}}-\frac{\textbf{1}}{\textbf{2}}\textbf{cos}^{\normalsize-1}\textbf{x.}$$
Sol. Let x cos θ so that cos–1 x = θ
$$\therefore\space \text{tan}^{\normalsize-1}\bigg(\frac{\sqrt{1 + x} - \sqrt{1 - x}}{\sqrt{1 +x} + \sqrt{1 - x}}\bigg)\\=\text{tan}^{\normalsize-1}\bigg(\frac{\sqrt{\text{1 + cos}\space\theta} - \sqrt{\text{1 - cos}\space \theta}}{\sqrt{\text{1 + cos}\space\theta} + \sqrt{\text{1 - cos}\theta}}\bigg)\\=\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\sqrt{2}\text{cos}\frac{\theta}{2} -\sqrt{2}\text{sin}\frac{\theta}{2}}{\sqrt{2}\text{cos}\frac{\theta}{2} + \sqrt{2}\text{sin}\frac{\theta}{2}}\end{pmatrix}$$
$$\begin{pmatrix}\because\space \text{1 + cos}\space\theta \text{= 2 cos}^{2}\frac{\theta}{2}\\\text{and}\space\text{1 - cos}\space\theta \text{= 2 sin}^{2}\frac{\theta}{2}\end{pmatrix}\\=\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\text{cos}\frac{\theta}{2} - \text{sin}\frac{\theta}{2}}{\text{cos}\frac{\theta}{2} + \text{sin}\frac{\theta}{2}}\end{pmatrix}\\=\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\text{1 - tan}\frac{\theta}{2}}{\text{1 + tan}\frac{\theta}{2}}\end{pmatrix}$$
(inside the bracket divide numerator and denominator by cos θ/2)
$$= \text{tan}^{\normalsize-1}\begin{bmatrix}\text{tan}\bigg(\frac{\pi}{4} -\frac{\theta}{2}\bigg)\end{bmatrix}\\\begin{bmatrix}\because\space \text{tan}(\text{A-B}) =\\\frac{\text{tan A - tan B}}{\text{1 + tan Atan B}}\end{bmatrix}\\=\frac{\pi}{4} -\frac{\theta}{2}=\frac{\pi}{2}-\frac{1}{2}\text{cos}^{\normalsize-1}x\\\textbf{Hence proved.}$$
$$\textbf{12.\space}\frac{\textbf{ 9}\pi}{\textbf{8}}\textbf{-}\frac{\textbf{9}}{\textbf{4}}\textbf{sin}^{\normalsize-1}\bigg(\frac{\textbf{1}}{\textbf{3}}\bigg)\\\textbf{=}\space\frac{\textbf{9}}{\textbf{4}}\textbf{sin}^{\normalsize-1}\bigg(\frac{\textbf{2}\sqrt{\textbf{2}}}{\textbf{3}}\bigg)\\\textbf{Sol.\space}\text{Given,\space}\frac{9\pi}{8}-\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg)\\=\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)\\\Rarr\space \frac{9\pi}{8} =\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg) +\\\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)$$
$$\Rarr\space\frac{9\pi}{8} =\frac{9}{4}\begin{bmatrix}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg) +\\\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)\end{bmatrix}\\\text{RHS} = \frac{9}{4}\begin{bmatrix}\text{sin}^{-1}\bigg(\frac{1}{3}\bigg) + \\\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)\end{bmatrix}\\=\frac{9}{4}\begin{bmatrix}\text{sin}^{\normalsize-1}\begin{Bmatrix}\frac{1}{3}\sqrt{1- \bigg(\frac{2\sqrt{2}}{3}\bigg)^{2}} +\\ \frac{2\sqrt{2}}{3}\sqrt{1 -\bigg(\frac{1}{3}\bigg)^{2}}\end{Bmatrix}\end{bmatrix}$$
$$\lbrack\because\space\text{sin}^{\normalsize-1} \text{x + sin}^{\normalsize-1}y\\=\text{sin}^{\normalsize-1}(x\sqrt{1 - y^{2}} + y\sqrt{1 - x^{2}})\rbrack\\=\frac{9}{4}\begin{bmatrix}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}×\frac{1}{3} + \frac{2\sqrt{2}}{3}×\frac{2\sqrt{2}}{3}\bigg)\end{bmatrix}\\=\frac{9}{4}\begin{bmatrix}\text{sin}^{\normalsize-1}\bigg(\frac{1}{9} +\frac{8}{9}\bigg)\end{bmatrix}\\=\frac{9}{4}\text{sin}^{\normalsize-1}(1)\\=\frac{9}{4}×\frac{\pi}{2} =\frac{9\pi}{8}=\text{LHS.}\\\textbf{Hence proved.}\\\textbf{Alternative method}\\\text{LHS} =\frac{9\pi}{8} -\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg)$$
$$=\frac{9}{4}\bigg(\frac{\pi}{2} -\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg)\bigg)\\=\frac{9}{4}\bigg(\text{cos}^{\normalsize-1}\bigg(\frac{1}{3}\bigg)\bigg)\\\bigg[\because\space\text{sin}^{\normalsize-1}x +\text{cos}^{\normalsize-1}x=\frac{\pi}{2}\bigg]\\=\frac{9}{4}\text{sin}^{\normalsize-1}\sqrt{1 - \bigg(\frac{1}{3}\bigg)^{2}}\\\lbrack\because\space\text{sin}^{\normalsize-1}x + \text{cos}^{\normalsize-1}x = \frac{\pi}{2}\rbrack\\=\frac{9}{4}\text{sin}^{\normalsize-1}\sqrt{1 - \bigg(\frac{1}{3}\bigg)^{2}}$$
$$\lbrack\because\space \text{cos}^{\normalsize-1}x =\text{sin}^{\normalsize-1}\sqrt{1 - x^{2}}\rbrack\\=\frac{9}{4}\text{sin}^{\normalsize-1}\sqrt{1 -\frac{1}{9}}\\=\frac{9}{4}\text{sin}^{\normalsize-1}\frac{2\sqrt{2}}{3}\space\text{ = RHS.}\\\textbf{Hence Proved.}$$
Solve the following equations :
13. 2 tan–1 (cos x) = tan–1 (2 cosec x).
Sol. Given, 2 tan–1 (cos x) = tan–1 (2 cosec x)
$$\Rarr\space\text{tan}^{\normalsize-1}\bigg(\frac{\text{2 cos x}}{\text{ 1 - cos}^{2}x}\bigg)\\=\text{tan}^{\normalsize-1}(\text{2 cosec x})\\\bigg[\because\space\text{2 tan}^{\normalsize-1}x = \text{tan}^{\normalsize-1}\bigg(\frac{2x}{1 - x^{2}}\bigg)\bigg]\\\Rarr\space \text{tan}^{\normalsize-1}\bigg(\frac{\text{2 cos x}}{\text{sin}^{2}x}\bigg)\\=\text{tan}^{\normalsize-1}\bigg(\frac{2}{\text{sin x}}\bigg)\\\Rarr\space \frac{\text{2cos x}}{\text{sin}^{2}x} =\frac{2}{\text{sin x}}\\\Rarr\space\frac{\text{2 cos x}}{\text{sin x}}= 2\\\Rarr\space\text{cot x = 1}$$
$$\Rarr\space\text{cot x = cot}\frac{\pi}{4}\\\Rarr\space x =\frac{\pi}{4}$$
$$\textbf{14.\space}\textbf{tan}^{\normalsize-1}\frac{\textbf{1-x}}{\textbf{1+x}} \textbf{=}\\\frac{\textbf{1}}{\textbf{2}}\textbf{tan}^{\normalsize-1}\textbf{x,}\textbf{(x}\gt\textbf{0).}$$
Sol. Given,
$$\text{tan}^{\normalsize-1}\bigg(\frac{\text{1 - x}}{\text{1 + x}}\bigg)\\=\frac{1}{2}\text{tan}^{\normalsize-1}x\\\text{or \space 2 tan}^{\normalsize-1}\bigg(\frac{\text{1 - x}}{\text{1 + x}}\bigg)\\=\text{tan}^{\normalsize-1}x \\\Rarr\space\text{tan}^{\normalsize-1}\begin{bmatrix}\frac{2\bigg(\frac{\text{1 - x}}{\text{1 + x}}\bigg)}{1 - \bigg(\frac{\text{1 - x}}{\text{1 + x}}\bigg)^{2}}\end{bmatrix}\\=\text{tan}^{\normalsize-1}x\\\bigg[\because\space\text{2 tan}^{\normalsize-1}y =\text{tan}^{\normalsize-1}\bigg(\frac{2y}{1 - y^{2}}\bigg)\bigg]$$
$$\Rarr\space\text{tan}^{\normalsize-1}\begin{bmatrix}\frac{\frac{2(1-x)}{(1 + x)}}{\frac{(1 + x^{2}) -(1 - x)^{2}}{(1 + x)^{2}}}\end{bmatrix}\\=\text{tan}^{\normalsize-1}x\\\Rarr\space\text{tan}^{\normalsize-1}\bigg[\frac{2(1-x)(1 + x)}{(1 + x)^{2} -(1 - x)^{2}}\bigg]\\=\text{tan}^{\normalsize-1}x\\\Rarr\space\text{tan}^{\normalsize-1}\bigg[\frac{2(1 - x)^{2}}{1^{2} + x^{2} + 2x - 1^{2} - x^{2} + 2x}\bigg]\\=\text{tan}^{\normalsize-1}x\\\Rarr\space\text{tan}^{\normalsize-1}\bigg[\frac{2(1 - x^{2})}{4x}\bigg]\\=\text{tan}^{\normalsize-1}x$$
$$\Rarr\space\text{tan}^{\normalsize-1}\bigg(\frac{(1 - x^{2})}{2x}\bigg)\\=\text{tan}^{\normalsize-1}x\\\Rarr\space\frac{1 - x^{2}}{2x} = x\\\Rarr\space 1-x^{2} = 2x^{2}\\\Rarr\space 1 = 3x^{2}\space\Rarr x^{2}=\frac{1}{3}\\\Rarr\space x=\pm\frac{1}{\sqrt{3}}\\\begin{bmatrix}\because\space x\gt 0\text{given, so we do not take}\\ x = -\frac{1}{\sqrt{3}}\end{bmatrix}\\\Rarr\space x=\frac{1}{\sqrt{3}}$$
15. sin (tan–1x), |x| < 1, is equal to :
$$\textbf{(a)}\frac{\textbf{x}}{\sqrt{\textbf{1 - x}^{2}}}\\\textbf{(b)\space}\frac{\textbf{1}}{\sqrt{\textbf{1 - x}^{\textbf{2}}}}\\\textbf{(c)\space}\frac{\textbf{1}}{\sqrt{\textbf{1 +x}^{\textbf{2}}}}\\\textbf{(d)\space}\frac{\textbf{x}}{\sqrt{\textbf{1 + x}^{2}}}\\\textbf{Sol.\space}\text{(d)}\space\frac{x}{\sqrt{1 + x^{2}}}\\\text{sin (tan}^{\normalsize–1}x) \\= \text{sin}\bigg[\text{sin}^{\normalsize-1}\frac{8}{\sqrt{1 + x^{2}}}\bigg]\\\bigg[\because\space \text{tan}^{\normalsize-1}x = \text{sin}^{\normalsize-1}\frac{x}{\sqrt{1 + x^{2}}}\bigg]$$
$$= \frac{x}{\sqrt{1 + x^{2}}}.$$
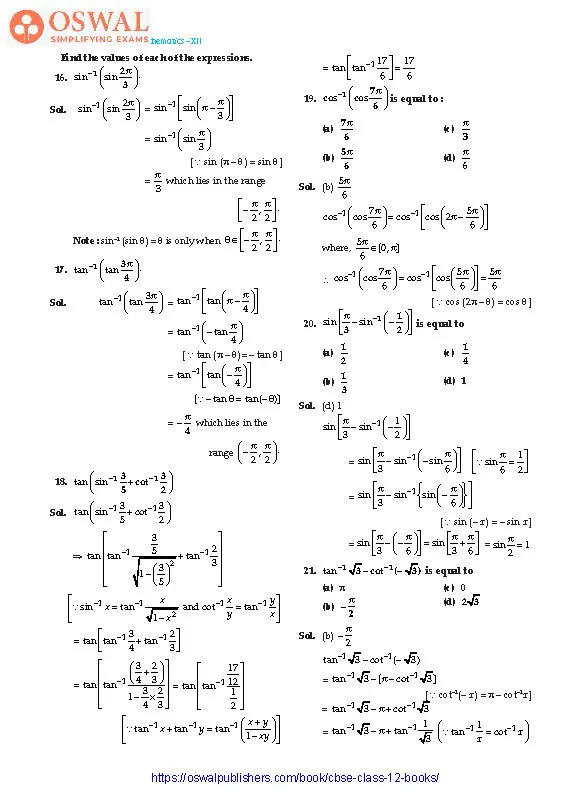
16. sin−1 (1 −x ) − 2sin−1
$$\textbf{x} = \frac{\pi}{\textbf{2}}\textbf{,}\\\textbf{then x is equal to}\\\textbf{(a) 0,}\frac{\textbf{1}}{\textbf{2}}\\\textbf{(b)\space 1,}\frac{\textbf{1}}{\textbf{2}}$$
(c) 0
$$\textbf{(d)}\space\frac{\textbf{1}}{\textbf{2}}$$
Sol. (c) 0
$$\text{Given, sin}^{\normalsize−1}(1− x) − 2sin^{\normalsize−1}x\\ = \frac{\pi}{2}\\\Rarr\space -\text{2 sin}^{-1}x = \frac{\pi}{2} -\text{sin}^{\normalsize-1}(1 - x)\\\Rarr\space\text{-2 sin}^{\normalsize-1}x = \text{cos}^{\normalsize-1}(1-x)\\\bigg[\because\space\text{sin}^{\normalsize-1}(1 -x) + \text{cos}^{\normalsize-1}(1 - x)=\frac{\pi}{2}\bigg]\\\Rarr\space\text{cos}\space(-2\text{sin}^{\normalsize-1}x) = 1-x $$
[Multiplying both sides by cos x]
$$\Rarr\space \text{cos}(2\space\text{sin}^{\normalsize-1}x)=1-x\\\lbrack\because\space\text{cos}(\normalsize-x) = +\space\text{cos x}\rbrack\\\Rarr\space[1 - 2\text{sin}^{2}(\text{sin}^{\normalsize-1}x)]=1-x\\\lbrack\because\space \text{cos 2x = 1-2\space\text{sin}}^{2}x\rbrack\\\Rarr\space 1 - 2x^{2}= 1 - x\\\Rarr\space 2x^{2}-x =0\\\Rarr\space x(2x-1) =0\\\Rarr\space x = 0$$
or 2x – 1 = 0
$$\Rarr\space x = 0 \space\text{or}\space\frac{1}{2}\\\text{But\space x = }\frac{1}{2}\space\text{does not satisfy}\\\text{the given equation, so x = 0.}\\ \textbf{Alternate method}\\\text{Given, sin}^{\normalsize-1}(1 - x) -\\ 2\text{sin}^{\normalsize-1}x=\frac{\pi}{2}$$
$$\text{Let x = sin}\space\theta\\\Rarr\space\theta = \text{sin}^{\normalsize-1}x,\space\text{then}\\\text{sin}^{\normalsize-1}(\text{1 - sin}\space\theta)- 2\theta =\frac{\pi}{2}\\\Rarr\space \text{sin}^{\normalsize-1}(\text{1 - sin}\space\theta) =\frac{\pi}{2} + 2\theta\\\Rarr\space \text{1 - sin}\space\theta =\text{sin}\bigg(\frac{\pi}{2} + 2\theta\bigg)\\\Rarr\space \text{1 - sin}\space\theta = \text{cos 2}\theta\\\bigg[\because\text{sin}\bigg(\frac{\pi}{2}+ \theta\bigg) =\text{cos}\theta\bigg]\\\Rarr\space\text{1 - sin}\space\theta = \text{1 - sin}^{2}\theta\\\lbrack\because\space \text{cos 2}\theta = 1- 2\text{sin}^{2}\theta\rbrack$$
$$\Rarr\space\text{2 sin}^{2}\theta -\text{sin}\space\theta =0\\\Rarr\space \text{sin}\space\theta(2 sin\theta-1)=0$$
Either sin θ = 0
or 2 sin θ – 1 = 0
$$\Rarr\space \text{x = 0}\space\text{or}\space\text{2x-1 =0}\\\lbrack\because\space\text{sin}\space\theta = x\rbrack\\\text{x =0 or x}=\frac{1}{2}\\\text{But\space x} =\frac{1}{2}\space\text{does not satisfy}$$
the given equation.
So, x = 0.
To check your answer.
Put x = 0 in the given equation,
$$\text{sin}^{\normalsize-1}(1 -0)- 2\space\text{sin}^{\normalsize-1} 0 =\frac{\pi}{2}\\\Rarr\space\frac{\pi}{2}-2×0 = \frac{\pi}{2}\\\Rarr\space \frac{\pi}{2}=\frac{\pi}{2}\\\text{Put}\space x =\frac{1}{2}\space\text{in the given equation,}\\\therefore\space\text{sin}^{\normalsize-1}\bigg(1 -\frac{1}{2}\bigg)-\\ 2\text{sin}^{\normalsize-1}\frac{1}{2}=\frac{\pi}{2}\\\therefore\space\text{sin}{\normalsize-1}\frac{1}{2} - 2\text{sin}^{\normalsize-1}\frac{1}{2}\\=\frac{\pi}{2}\\\Rarr\space \frac{\pi}{6}-2×\frac{\pi}{6} =\frac{\pi}{2}$$
$$\Rarr\space \frac{\pi - 2\pi}{6}=\frac{\pi}{2}\\\Rarr\space \frac{-\pi}{6}\neq\frac{\pi}{2},\\\text{So \space x =}\frac{1}{2}\space\text{is not possible.}$$
Note : While solving the trigonometric equation, sometimes it may have some extra roots, so please take careful about it.
$$\textbf{17.\space tan}^{\normalsize-1}\bigg(\frac{\textbf{x}}{\textbf{y}}\bigg) \textbf{- tan}^{\normalsize-1}\bigg(\frac{\textbf{x-y}}{\textbf{x+y}}\bigg)\\\textbf{is equal to}$$
$$\textbf{(a)\space}\frac{\pi}{\textbf{2}}\\\textbf{(b)\space}\frac{\pi}{\textbf{3}}\\\textbf{(c)\space}\frac{\pi}{\textbf{4}}\\\textbf{(d)\space}\frac{\textbf{3}\pi}{\textbf{4}}\\\textbf{Sol.\space}(c)\frac{\pi}{4}\\\text{tan}^{\normalsize-1}\bigg(\frac{x}{y}\bigg) -\text{tan}^{\normalsize-1}\bigg(\frac{x-y}{x + y}\bigg)\\=\text{tan}^{\normalsize-1}\bigg(\frac{x}{y}\bigg)-\text{tan}^{\normalsize-1}\begin{pmatrix}\frac{\frac{x}{y}-1}{\frac{x}{y}+1}\end{pmatrix}\\=\text{tan}^{\normalsize-1}\bigg(\frac{x}{y}\bigg) -\\\begin{Bmatrix}\text{tan}^{\normalsize-1}\frac{x}{y} - \text{tan}^{\normalsize-1}1\end{Bmatrix}$$
$$\bigg[\because\space\text{tan}^{\normalsize-1}x - \text{tan}^{\normalsize-1}y=\\\text{tan}^{\normalsize-1}\bigg(\frac{x-y}{\text{1 + xy}}\bigg)\bigg]\\=\text{tan}^{\normalsize-1}1 =\frac{\pi}{4}.$$
