NCERT Solutions for Class 12 Maths Chapter 8 - Applications of Integrals - Exercise 8.1

Access Exercises of Class 12 Maths Chapter 8 – Applications of the Integrals

Exercise 8.1 Solutions: 13 Questions (8 Long, 3 Short, 2 MCQs)

Exercise 8.2 Solutions: 7 Questions(5 Long, 2 MCQs)

Miscellaneous Exercise Solutions: 19 Questions (8 Long, 7 Short, 4 MCQs)

Exercise 8.1

1. Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4 and the X-axis in the first quadrant.

Sol. The area of the region bounded by the curve, y² = x, the lines x = 1 and x = 4 and the X-axis is shown in the figure.

Here

Since, the given curve y² = x is parabola which is symmetrical about X-axis (∵ it contains even power of y) and passes through the origin.

Required area (shaded region)

$$=\int^{b}_{a}|y|dx\\=\int^{4}_{1}|y|dx = \int^{4}_{1}\sqrt{x}dx\\(\because\space y^{2} = x, \because\space |y|=\sqrt{x})\\=\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{4}_{1}=\frac{2}{3}\lbrack4^{\frac{3}{2} -}1^{\frac{3}{2}}\rbrack\\\bigg[\because\space\int x^{n}=\frac{x^{n+1}}{\text{n+1}}\bigg]\\=\frac{2}{3}\lbrack(2^{2})^{\frac{3}{2}}-1\rbrack=\frac{2}{3}\lbrack8-1\rbrack\\=\frac{14}{3}\text{sq units} $$

Note : We can solve these questions without drawing the curve.

2. Find the area of the region bounded by y² = 9x, x = 2, x = 4 and the X-axis in the first quadrant.

Sol. Since, the given curve y² = 9x is a parabola which is symmetrical about x-axis (∵ the power of y is even) and passes through the origin.

The area of the region bounded by the curve, y² = 9x, x = 2 and x = 4 and the X-axis is the area shown in the figure.

Required area (shaded region)

$$=\int^{4}_{2}|y|dx\\=\int^{4}_{2}3\sqrt{x}dx\space\\(\because\space y^{2}=9x\Rarr\space |y|=3\sqrt{x})\\=3\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{4}_{2}=\frac{3×2}{3}\lbrack4^{\frac{3}{2}-}2^{\frac{3}{2}}\rbrack\\=2\lbrack4\sqrt{4} - 2\sqrt{2}\rbrack\\=2\lbrack 8-2\sqrt{2}\rbrack\\= 4\lbrack 4-\sqrt{2}\rbrack\text{sq unit}$$

3. Find the area of the region bounded by x² = 4y, y = 2, y = 4 and the Y-axis in the first quadrant.

Sol. The given curve x² = 4y is a parabola which is symmetrical about Y-axis (∵ It contains even power of x) only and passes through the origin.

The area of the region bounded by the curve x² = 4y, y = 2 and y = 4 and the Y-axis is shown in the figure.

Required area (shaded region) =

$$\int^{\text{y=b}}_{\text{y=a}}|x|dy\\(\text{Here,\space |x|=}\sqrt{4 y}\space \text{and a=2, b=4})\\=\int^{4}_{2}|x|dy$$

(Considering the elementary strip on Y-axis)

$$=\int^{4}_{2} 2\sqrt{y}\space dy\\\space(\because\space x^{2}=4y\space \therefore\space |x|=2\sqrt{y})\\=2\bigg[\frac{y^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{4}_{2}=\frac{4}{3}\lbrack 4^{\frac{3}{2}}-2^{\frac{3}{2}}\rbrack\\=\frac{4}{3}\lbrack8-2\sqrt{2}\rbrack=\frac{8}{3}\lbrack4-\sqrt{2}\rbrack\text{sq unit}$$

4. Find the area of the region bounded by the ellipse

$$\frac{\textbf{x}^{\textbf{2}}}{\textbf{16}}+\frac{\textbf{x}^{\textbf{2}}}{\textbf{16}}\textbf{= 1.}$$

Sol. The given curve is an ellipse with centre at (0, 0) and symmetrical about X-axis and Y-axis (∵ the power of x and y both are even).

Area bounded by the ellipse

= 4 × (Area of shaded region in the first quadrant only)

(∵ By symmetry)

$$= 4 ×\int^{\text{x=b}}_{\text{x=a}}|y|dx = 4\int^{4}_{0}|y|dx\\=4\int^{4}_{0}\frac{3}{4}\sqrt{16-x^{2}}dx\\\bigg(\because\space\frac{x^{2}}{16} + \frac{y^{2}}{9}=1\therefore\space |y|=\frac{3}{4}\sqrt{16-x^{2}}\bigg)\\= 3\int^{4}_{0}\sqrt{4^{2}-x^{2}}dx\\= 3\bigg[\frac{x}{2}\sqrt{4^{2}-x^{2}} + \frac{4^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{4}\bigg)\bigg]^{4}_{0}\\\begin{bmatrix}\because\int\sqrt{a^{2}-x^{2}}dx=\frac{x}{a}\sqrt{a^{2}-x^{2}}+\\\frac{a^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{a}\bigg)\end{bmatrix}$$

$$= 3\lbrack 2\sqrt{16-16} + 8\text{sin}^{\normalsize-1}(1)-0-8\\-\text{sin}^{\normalsize-1}(0)\rbrack\\=3 \lbrack 0 + 8 \space\text{sin}^{\normalsize-1}(1)-0\rbrack\\3×8×\bigg(\frac{\pi}{2}\bigg)=12\pi\space\text{sq unit}$$

Therefore, area bounded by the ellipse is 12 p sq. units.

Note : If we take elementary strip about either X or Y-axis, in both cases the area should be same.

5. Find the area of the region bounded by the ellipse

$$\frac{\textbf{x}^{\textbf{2}}}{\textbf{4}}\textbf{+}\frac{\textbf{y}^{\textbf{2}}}{\textbf{9}}\textbf{= 1.}$$

Sol. The given curve is an ellipse with centre at (0, 0) and symmetrical about X-axis and Y-axis.

Area bounded by the ellipse

= 4 × (Area of shaded region in the first quadrant only)

(∵ By symmetry)

$$= 4×\int^{x=b}_{x=a}|y|dx\\= 4\int^{2}_{0}|y|dx= 4\int^{2}_{0}\frac{3}{2}\sqrt{4-x^{2}}dx\\\bigg(\because\space \frac{x^{2}}{4}+\frac{y^{2}}{9}=1\space\therefore\space |y|=\frac{3}{2}\sqrt{4-x^{2}}\bigg)$$

$$= 6\int^{2}_{0}\sqrt{2^{2}-x^{2}}dx=\\6\bigg[\frac{x}{2}\sqrt{4-x^{2}} + \frac{2^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{2}\bigg)\bigg]^{2}_{0}\\\begin{bmatrix}\because\int\sqrt{a^{2}-x^{2}}dx = \frac{x}{2}\sqrt{a^{2}-x^{2}}+\\\frac{a^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{a}\bigg)\end{bmatrix}\\=6\lbrack 0 +2\space\text{sin}^{\normalsize-1}(1)-0\rbrack\\=6×2×\bigg(\frac{\pi}{2}\bigg)=6\pi\space\text{sq unit}$$

6. Find the area of the region in the first quadrant enclosed by X-axis, line

$$\textbf{x = }\sqrt{\textbf{3}}\textbf{y}\space\textbf{and the circle x}^{\textbf{2}} \textbf{+ y}^\textbf{2} \textbf{= 4.}$$

Sol. Firstly find the intersection point of

$$x=\sqrt{3}\space\text{and}\space x^{2}+y^{2}=4$$

in the first quadrant and then draw a rough diagram to indicate the required area.

Now, divide the area into two parts one lying under the line joining point of intersection to (0, 0) and other lying under the circle and then integrate separately to find required area.

$$\text{Given equation of circle is}\\ x^{2}+y^{2}=4\space\text{and} x=\sqrt{3}y\\\text{or \space} y=\frac{1}{\sqrt{3}}x\space\text{represents a line}\\\text{through the origin.}\\\text{The line y}=\frac{1}{\sqrt{3}}x\space\text{intersect the circle so it will\space}\\\text{satisfy the equation of circle}\\\therefore\space x^{2}+\bigg(\frac{1}{\sqrt{3}}x\bigg)^{2}=4\\\Rarr\space\frac{4}{3}x^{2}=4$$

$$\Rarr\space x^{2}=\frac{4×3}{4}=3\\\Rarr\space x=\pm\sqrt{3}\\\text{when x}=\sqrt{3}\space\text{then y}=\frac{1}{\sqrt{3}}(\sqrt{3})=1.\\\lbrack\text{For first quadrant we take }\\x =\sqrt{3}\space\text{and neglect}\space x=-\sqrt{3}\rbrack\\\therefore\space\text{The line and the circle meet at the point}\\(\sqrt{3},1).$$

Required area (shaded region in first quadrant)

$$= \text{Area under the line y =}\frac{1}{3}x\space\\\text{from x=0}\space \text{to x=}\sqrt{3} + \\\text{Area under the circle from x =}\sqrt{3}\space\text{to x=2})$$

$$=\int^{\sqrt{3}}_{0}\frac{1}{\sqrt{3}}\text{ x dx} + \int^{2}_{\sqrt{3}}\sqrt{4- x^{2}}dx\\(\because\space x^{2} + y^{2}=4\Rarr\space y=\sqrt{4-{x}^{2}})\\=\frac{1}{\sqrt{3}}.\bigg[\frac{x^{2}}{2}\bigg]^{\sqrt{3}}_{0} + \bigg[\frac{x}{2}\sqrt{4-x^{2} } + \frac{2^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{2}\bigg)\bigg]^{2}_{\sqrt{3}}$$

$$=\frac{1}{2\sqrt{3}}\lbrack(\sqrt{3})^{2}-0^{2}\rbrack + \begin{bmatrix}0 + 2\space\text{sin}^{\normalsize-1}(1)-\\\frac{\sqrt{3}}{2}\sqrt{4-3}-2\text{sin}^{\normalsize-1}\bigg(\frac{\sqrt{3}}{2}\bigg)\end{bmatrix}\\=\frac{\sqrt{3}}{2}+2\bigg(\frac{\pi}{2}\bigg)-\frac{\sqrt{3}}{2}-2\bigg(\frac{\pi}{3}\bigg)\\=\pi - \frac{2\pi}{3}=\frac{\pi}{3}\text{sq unit}$$

7. Find the area of the smaller part of the circle x² + y² = a² cut-off by the line

$$\textbf{x =} \frac{\textbf{a}}{\sqrt{\textbf{2}}}. $$

$$\textbf{Sol.\space}\text{Given line,}\space x=\frac{a}{\sqrt{2}}\space\text{...(i)}$$

and circle, x² + y² = a² ...(ii)

Since, given line cuts the circle so put

$$x=\frac{a}{\sqrt{2}}\space\text{in equation (ii), we get}\\\bigg(\frac{a}{\sqrt{2}}\bigg)^{2}+y^{2}=a^{2}\\\Rarr\space y^{2} = \frac{a^{2}}{1}-\frac{a^{2}}{2}=\frac{a^{2}}{2}\\\Rarr\space |y|= \frac{a}{\sqrt{2}},\Rarr\space y \pm\frac{a}{\sqrt{2}} $$

$$\text{When}\space y = \frac{a}{\sqrt{2}}, x^{2}= a^{2}-\bigg(\frac{a^{2}}{2}\bigg)\\\Rarr\space x^{2}=\frac{a^{2}}{2}\Rarr\space x = \pm\frac{a}{\sqrt{2}}\\\therefore\space\text{Intersection point in first quadrant is}\\\bigg(\frac{a}{\sqrt{2}},\frac{a}{\sqrt{2}}\bigg)$$

Required area

= 2 (Area of shaded region in first quadrant only)

$$= 2\int^{a}_{\frac{a}{\sqrt{2}}}|y|dx = 2\int^{a}_{\frac{a}{\sqrt{2}}}\sqrt{a^{2}-x^{2}}\space dx\\=2\bigg[\frac{x}{2}\sqrt{a^{2}-x^{2}} + \frac{a^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{a}\bigg)\bigg]^{a}_{\frac{a}{\sqrt{2}}}$$

$$\begin{bmatrix}\because\space \int\sqrt{a^{2}-x^{2}}dx=\frac{x}{2}\sqrt{a^{2}-x^{2}} +\\\frac{a^{2}}{2}\text{sin}{\normalsize-1}\bigg(\frac{x}{a}\bigg)\end{bmatrix}\\=2\begin{bmatrix} 0 + \frac{a^{2}}{2}\text{sin}^{\normalsize-1}(1)-\frac{a}{2\sqrt{2}}\sqrt{a^{2}-\frac{a^{2}}{2}-}\\\frac{a^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{1}{\sqrt{2}}\bigg)\end{bmatrix}$$

$$= 2\bigg[\frac{a^{2}}{2}\bigg(\frac{\pi}{2}\bigg) - \frac{a}{2\sqrt{2}}.\frac{a}{\sqrt{2}}-\frac{a^{2}}{2}\bigg(\frac{\pi}{4}\bigg)\bigg]\\=2\bigg[\frac{a^{2}\pi}{4}-\frac{\pi a^{2}}{8}-\frac{a^{2}}{4}\bigg]=\\\bigg(\frac{a^{2}\pi}{4}-\frac{a^{2}}{2}\bigg)\\=\frac{a^{2}}{2}\bigg(\frac{\pi}{2}-1\bigg)\space\text{sq unit}$$

Therefore, the area of smaller part of the circle,

x² + y² = a², cut-off by the line,

$$x = \frac{a}{\sqrt{2}},\space\text{is}\space\frac{a^{2}}{2}\bigg(\frac{\pi}{2}-1\bigg)\space\text{sq unit.}$$

8. The area between x = y² and x = 4 is divided into two equal parts by the line x = a, find the value of a.

Sol. Given curve x = y² is a parabola symmetrical about X-axis and passing through the origin.

The line x = a, divides the area bounded by the parabola and x = 4 into two equal parts.

Area OAD = Area ABCD

∴ Area OED = Area EFCD

$$\Rarr\space\text{Area OED}=\int^{a}_{0}\text{y dx}\\\text{and\space area of EFCD = }\int^{4}_{a}\sqrt{x}\space dx\\(\because\space y^{2}=x\Rarr\space |y|=\sqrt{x})\\\Rarr\space\int^{a}_{0}\sqrt{x}\space dx=\int^{4}_{a}\sqrt{x}dx\\\Rarr\space\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{a}_{0}=\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{4}_{a}\\\Rarr\space\frac{2}{3}\lbrack a^{\frac{3}{2}}-0\rbrack=\frac{2}{3}\lbrack 4^{\frac{3}{2}}-a^{\frac{3}{2}}\rbrack\\\Rarr\space a^{\frac{3}{2}}= 4^{\frac{3}{2}}-a^{\frac{3}{2}}\\\Rarr\space 2a^{\frac{3}{2}}=8\\\Rarr\space a^{\frac{3}{2}}=4$$

$$\Rarr\space a = (4)^{\frac{2}{3}}\\\text{Therefore, the value of a is}\space(4)^{\frac{2}{3}}.$$

9. Find the area of the region bounded by the parabola y = x² and y |x|.

Sol. Firstly draw the curve y = x² and line y = |x|

$$=\begin{cases}x, x\gt 0\\0, x=0\\-x, x\lt0.\end{cases}$$

The common shaded region is the required area.

Given parabola y = x² which is symmetrical about Y-axis and passes through (0, 0) and the curve y = |x|.

On putting x = – x, we get

y = |– x| = |x|

∴ Curve y = |x| is symmetrical about Y-axis and passes through origin.

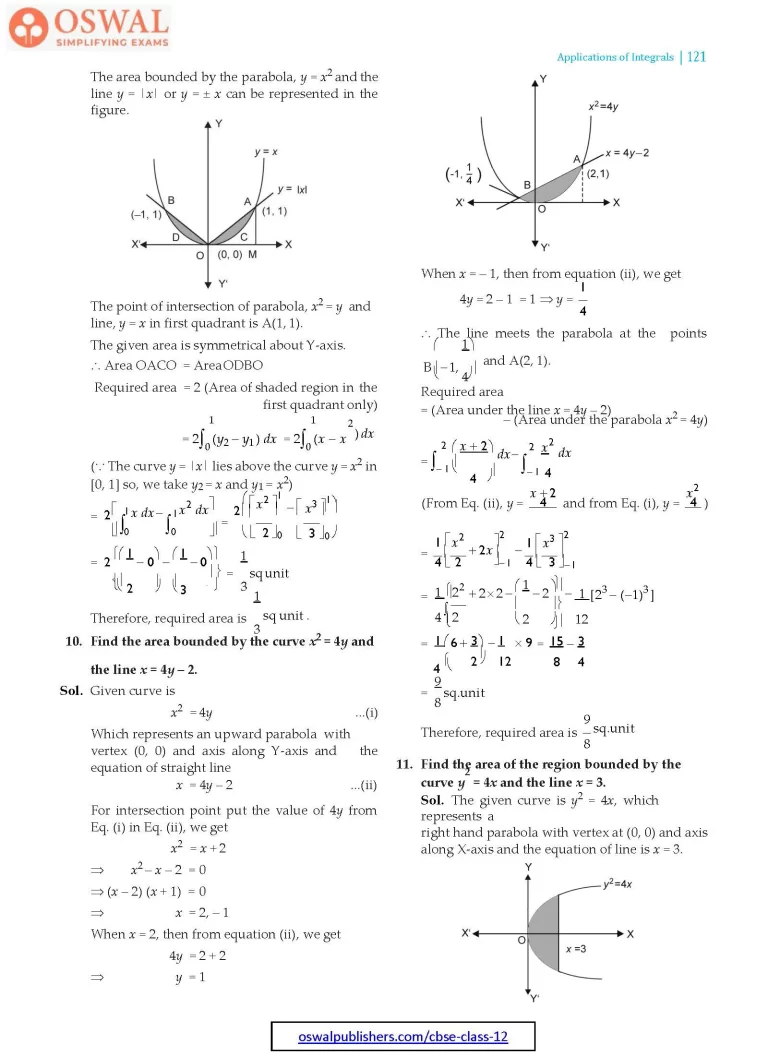
The area bounded by the parabola, y = x² and the line y = |x| or y = ± x can be represented in the figure.

The point of intersection of parabola, x² = y and line, y = x in first quadrant is A(1, 1).

The given area is symmetrical about Y-axis.

∴ Area OACO = Area ODBO

Required area = 2 (Area of shaded region in the first quadrant only)

$$= 2\int^{1}_{0}(y_2-y_1)dx=2\int^{1}_{0}(x-x^{2})dx$$

(∵ The curve y = |x| lies above the curve y = x² in [0, 1] so, we take y₂ = x and y₁ = x²)

$$= 2\bigg[\int^{1}_{0} x dx - \int^{1}_{0} x^{2}dx\bigg]\\= 2\bigg(\bigg[\frac{x^{2}}{2}\bigg]^{1}_{0} - \bigg[\frac{x^{3}}{3}\bigg]^{1}_{0}\bigg)\\= 2\begin{Bmatrix}\bigg(\frac{1}{2}-0\bigg) -\bigg(\frac{1}{3}-0\bigg)\end{Bmatrix}\\=\frac{1}{3}\text{sq unit}\\\text{Therefore, required area is}\space\frac{1}{3}\space\text{sq unit.}$$

10. Find the area bounded by the curve x² = 4y and the line x = 4y – 2.

Sol. Given curve is

x² = 4y ...(i)

Which represents an upward parabola with vertex (0, 0) and axis along Y-axis and the equation of straight line

x = 4y – 2 ...(ii)

For intersection point put the value of 4y from Eq. (i) in Eq. (ii), we get

x² = x + 2

$$\Rarr\space x^{2}-x-2=0\\\Rarr\space (x-2)(x+1)=0\\\Rarr\space x=2,\normalsize-1$$

When x = 2, then from equation (ii), we get

4y = 2 + 2

$$\Rarr\space y=1$$

When x = – 1, then from equation (ii), we get

$$\text{4y = 2-1 = 1}\\\Rarr y=\frac{1}{4}$$

∴ The line meets the parabola at the points

$$\text B\bigg(-1,\frac{1}{4}\bigg)\space\text{and A(2,1).}$$

Required area

= (Area under the line x = 4y – 2)
– (Area under the parabola x² = 4y)

$$=\int^{2}_{\normalsize-1}\bigg(\frac{x+2}{4}\bigg)dx-\int^{2}_{\normalsize-1}\frac{x^{2}}{4}dx\\\text{(from Eq. (ii) y = )}\frac{x+2}{4}\\\text{and from Eq.(i) y = }\frac{x^{2}}{4})\\=\frac{1}{4}\bigg[\frac{x^{2}}{2} + 2x\bigg]^{2}_{\normalsize-1}-\frac{1}{4}\bigg[\frac{x^{3}}{3}\bigg]^{2}_{\normalsize-1}\\=\frac{1}{4}\begin{Bmatrix}\frac{2^{2}}{2}+2×2-\bigg(\frac{1}{2}-2\bigg)-\end{Bmatrix}\\-\frac{1}{12}\lbrack2^{3}-(-1)^{3}\rbrack\\=\frac{1}{4}\bigg(6 +\frac{3}{2}\bigg)-\frac{1}{12}×9$$

$$=\frac{15}{8}-\frac{3}{4}\\=\frac{9}{8}\text{sq. unit}\\\text{Therefore, required area is}\space\frac{9}{8}\space\text{sq. unit}$$

11. Find the area of the region bounded by the curve y² = 4x and the line x = 3.

Sol. The given curve is y² = 4x, which represents a right hand parabola with vertex at (0, 0) and axis along X-axis and the equation of line is x = 3.

Required area

= 2 × (Area of shaded region in the first quadrant only)

$$= 2\int^{3}_{0}|y|dx\\= 2\int^{3}_{0}2\sqrt{x}dx\\(\because\space y^{2}=4x \Rarr y=2\sqrt{x})\\= 4\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{3}_{0}=\frac{8}{3}\lbrack 3^{\frac{3}{2}}-0\rbrack\\=\frac{8}{3}(3\sqrt{3})= 8\sqrt{3}\text{sq unit.}\\\text{Therefore, the required area is}\\\space\text{8}\sqrt{3}\text{sq unit}$$

Choose the correct answer in the following.

12. Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is :

$$\textbf{(a)\space}\pi\\\textbf{(b)\space}\frac{\pi}{2}\\\textbf{(c)\space}\frac{\pi}{3}\\\textbf{(d)\space}\frac{\pi}{4}\\\textbf{Sol.}\space \text{(a)}\space\pi$$

The area bounded by the circle and the lines x = 0 and x = 2, in the first quadrant is represented in the figure by shaded region.

$$\text{Required area =}\int^{2}_{0}|y|dx\\=\int^{2}_{0}\sqrt{4-x^{2}}dx\\=\bigg[\frac{x}{2}\sqrt{4-x^{2}} + \frac{4}{2}\text{tan}^{\normalsize-1}\bigg(\frac{x}{2}\bigg)\bigg]^{2}_{0}\\= 0 + 2\space\text{sin}^{\normalsize-1}(1)-0\\= 2×\frac{\pi}{2}$$

= π sq unit

13. Area of the region bounded by the curve y² = 4x, Y-axis and the line y = 3 is :

$$\textbf{(a)\space 2}\\\textbf{(b)\space}\frac{9}{4}\\\textbf{(c)\space}\frac{9}{3}\\\textbf{(d)}\frac{9}{2}\\\textbf{Sol.}\space\text{(b)}\frac{9}{4}$$

The area bounded by the curve, y² = 4x, Y-axis and y = 3 is represented in the figure by shaded region.

$$\text{Required area}=\int^{3}_{0}|x|dy\\=\int^{3}_{0}\frac{y^{2}}{4}dy\\=\frac{1}{4}\bigg[\frac{y^{3}}{3}\bigg]^{3}_{0}=\frac{1}{12}(3^{3}-0)\\=\frac{1}{12}(27)=\frac{9}{4}\space\text{sq unit.}$$

Download PDF