NCERT Solutions for Class 12 Maths Chapter 8 - Applications of Integrals - Miscellaneous Exercise







Access Exercises of Class 12 Maths Chapter 8 – Applications of the Integrals
Exercise 8.1 Solutions: 13 Questions (8 Long, 3 Short, 2 MCQs)
Exercise 8.2 Solutions: 7 Questions(5 Long, 2 MCQs)
Miscellaneous Exercise Solutions: 19 Questions (8 Long, 7 Short, 4 MCQs)
Miscellaneous Exercise
1. Find the area under the given curves and given lines.
(a) y = x2; x = 1, x = 2 and X-axis
(b) y = x4; x = 1, x = 5 and X-axis.
Sol. (a) The given curve y = x2 represents an upward parabola with vertex (0, 0) and axis along Y-axis.
∴ Required area (shown in shaded region)

= Area under the curve y = x2,
X-axis and x = 1, x = 2
$$=\int^{2}_{1} ydx = \int^{2}_{1}x^{2}dx=\\\bigg[\frac{x^{3}}{3}\bigg]^{2}_{1}=\frac{1}{3}\lbrack2^{3}-1^{3}\rbrack\\=\frac{8}{3}-\frac{1}{3}=\frac{7}{8}\text{sq unit}$$
(b) Given, y = x4,
Here, x is even, so curve is symmetrical about Y-axis and passes through origin (0, 0).

∴ Required area
= Area under the curve y = x4, X-axis and x = 1, x = 5
$$=\int^{5}_{1}x^{4}dx= \bigg[\frac{x^{5}}{5}\bigg]^{5}_{1}\\=\frac{1}{5}\lbrack 5^{5}-1\rbrack\\=\frac{1}{5}(3125-1)=\frac{3124}{5}\\=624.8\space\text{sq.unit}$$
2. Find the area between the curves y = x and y = x2.
Sol. Given, curve [represents an upward parabola with vertex (0, 0)]
x2 = y ...(i)
and equation of the line y = x ...(ii)
For intersection point x2 = x
[From Eqs. (i) and (ii)]
$$\Rarr\space x(x-1)=0\\\Rarr\space x=0,1$$

When x = 0, y = 0 and when x = 1, y = 1.
Thus, point of intersection of parabola and line are (0, 0) and (1, 1).
$$\therefore\space\text{Required area =}\int^{1}_{0}(y_2-y_1)dx\\=\int^{1}_{0}(x-x^{2})dx\\=\bigg[\frac{x^{2}}{2}-\frac{x^{3}}{3}\bigg]^{1}_{0}=\bigg(\frac{1}{2}-\frac{1}{3}\bigg)-0\\=\frac{1}{6}\text{sq unit}$$
3. Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4.
Sol. The area in the first quadrant bounded by y = 4x2, y = 4, x = 0, y = 1 is represented by the shaded region.

∴ Required area (shown in shaded region)
$$=\int^{4}_{1}|x|dy\\=\int^{4}_{1}\frac{1}{2}\sqrt{y}dy\\\bigg(\because\space y= 4x^{2}\space\therefore\space x^{2}=\frac{y}{4}\Rarr|x|=\frac{\sqrt{y}}{2}\bigg)\\=\frac{1}{2}\bigg[\frac{y^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{4}_{1}\\=\frac{1}{3} (4^{\frac{3}{2}}-1^{\frac{3}{2}})=\frac{1}{3}\lbrack(2^{2})^{\frac{3}{2}}-1\rbrack\\=\frac{1}{3}(8-1)\\=\frac{7}{8}\text{sq unit}$$
4. Sketch the graph of y = |x + 3| and evaluate
$$\int^{\textbf{0}}_{\textbf{\normalsize -6}}\textbf{|x+3|dx.}\\\textbf{Sol.\space} y=|x+3|=\begin{cases}-(x+3)\text{for x}\lt-3\\ x+3\space\text{for x}\geq -3\end{cases}$$
When x < – 3, y = – x – 3
| x | -4 | -5 | -6 |
| y | 1 | 2 | 3 |
$$\text{When x}\geq -3$$
| x | -1 | -2 | -3 |
| y | 2 | 1 | 0 |
Draw these points on the graph paper and we get the required figure.
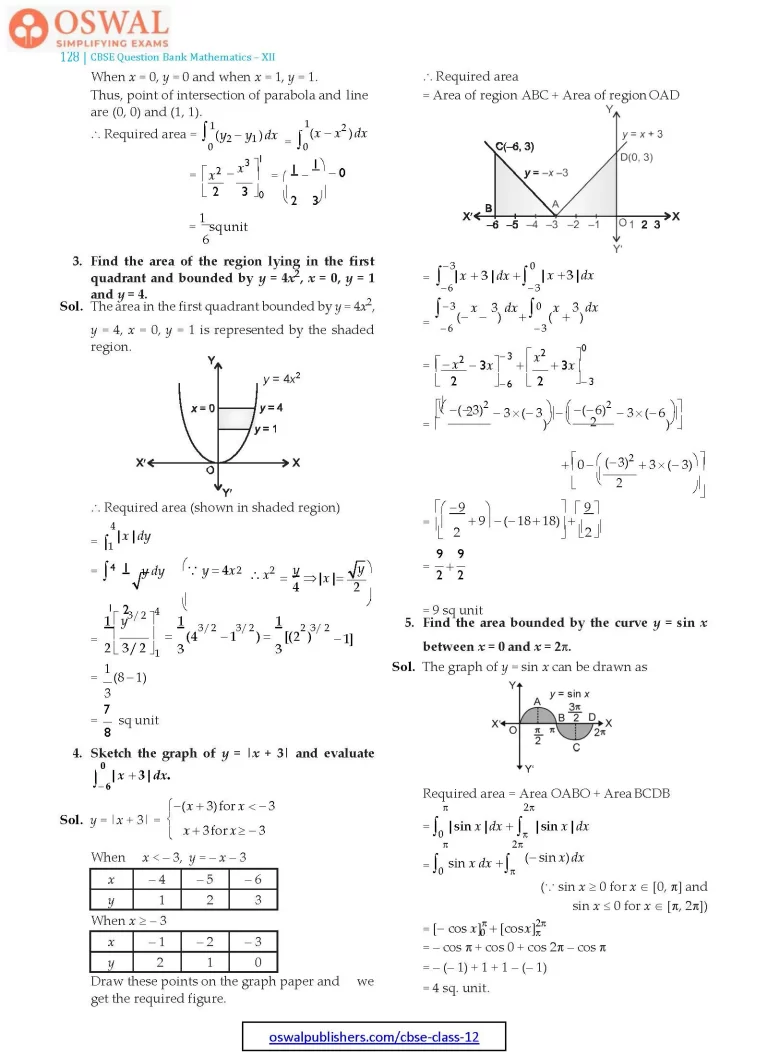
∴ Required area
= Area of region ABC + Area of region OAD

$$= \int^{\normalsize-3}_{\normalsize-6}|x+3|dx + \int^{0}_{\normalsize-3}|x+3|dx\\=\int^{-3}_{-6}(-x-3)dx+\int^{0}_{\normalsize-3}(x+3)dx\\=\bigg[\frac{-x^{2}}{2}-3x\bigg]^{-3}_{-6} + \bigg[\frac{x^{2}}{2} + 3x\bigg]^{0}_{\normalsize-3}\\=\begin{bmatrix}\bigg(\frac{-(-3)^{2}}{2}-3×(\normalsize-3)\bigg)-\\\bigg(\frac{-(-6)^{2}}{3}-3×(-6)\bigg)\end{bmatrix}\\+\bigg[0-\bigg(\frac{(\normalsize-3)^{2}}{2}+3×(\normalsize-3)\bigg)\bigg]$$
$$=\bigg[\bigg(\frac{-9}{2}+9\bigg) - (-18+18)\bigg]+\bigg[\frac{9}{2}\bigg]\\=\frac{9}{2}+\frac{9}{2}$$
= 9 sq unit
5. Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Sol. The graph of y = sin x can be drawn as

Required area = Area OABO + Area BCDB
$$=\int^{\pi}_{0}|\text{sin x}|dx + \int^{2\pi}_{\pi}|\text{sin x}|dx\\=\int^{\pi}_{0}\text{sin x dx} + \int^{2\pi}_{\pi}(-\text{sin x})dx\\(\because\space\text{sin x}\geq 0\space\text{for x}\epsilon\lbrack0,\pi\rbrack\space\text{and}\space\\\text{sin x}\leq 0 \text{for x}\epsilon\lbrack\pi,2\pi\rbrack)\\=\lbrack\text{- cos x}\rbrack^{\pi}_{0} + \lbrack\text{cos x}\rbrack^{2\pi}_{\pi}$$
= – cos π + cos 0 + cos 2π – cos π
= – (– 1) + 1 + 1 – (– 1)
= 4 sq. unit.
6. Find the area enclosed between the parabola
y2 = 4ax and the line y = mx.
Sol. Given, the curve [represents a parabola with vertex (0, 0)]
y2 = 4ax ...(i)
and equation of line
y = mx ...(ii)
From equations (i) and (ii), we get
(mx)2 = 4ax
$$\Rarr\space x(m^{2}x-4a)=0\\\Rarr\space x=0\space\text{or}\space x = \frac{4a}{m^{2}}\\\text{When x = 0, y = m × 0 = 0,}\\\text{When}\space x=\frac{4a}{m^{2}}, y=m×\frac{4a}{m^{2}}=\frac{4a}{m}$$
∴ The points of intersection of both the curves are (0, 0) and
$$\bigg(\frac{4a}{m^{2}},\frac{4a}{m}\bigg)$$

∴ Required area
$$= \int^{\frac{4a}{m^{2}}}_{0}(\sqrt{4ax}-mx)dx\\(... y^{2}=4ax... y=\sqrt{4ax}\\\text{in the first quadrant})\\= 2\sqrt{a}\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{\frac{4a}{m^{2}}}_{0}-\bigg[m\frac{x^{2}}{2}\bigg]^{\frac{4a}{m^{2}}}_{0}\\=\frac{4}{3}\sqrt{a}\bigg(\frac{4a}{m^{2}}\bigg)^{\frac{3}{2}}-\frac{m}{2}\bigg(\frac{4a}{m^{2}}\bigg)^{2}\\=\frac{4}{3}\sqrt{a}.\bigg(\frac{4a}{m^2}\bigg)\sqrt{\frac{4a}{m^{2}}}-\frac{m(16a^{2})}{2m^{4}}\\=\frac{32}{3}.\frac{a^{2}}{m^{3}}-\frac{8a^{2}}{m^{3}}=\frac{8a^{2}}{3m^{3}}$$
7. Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12.
Sol. Given the curve [represents an upward parabola with vertex (0, 0)]
4y = 3x2 ...(i)
and equation of line
2y = 3x + 12 ...(ii)
For intersection point from equations (i) and (ii), we get
2(3x + 12) = 3x2
$$\Rarr\space 3x^{2}-6x-24=0\\\Rarr\space x^{2}-2x-8=0\\\Rarr\space (x-4)(x+2)=0\Rarr\space x=4,-2\\\text{When\space x=4, y=}\frac{3×4+12}{2}=12\\\text{When\space x = -2, y=}\frac{3×(\normalsize-2)+12}{2}=3$$

Thus, intersection points are (– 2, 3) and (4, 12).
Required area (shown in shaded region)
= (Area under the line between x = – 2 and x = 4)– (Area under the parabola between x = – 2 and x = 4)
$$=\int^{4}_{\normalsize-2}\bigg(\frac{3x+12}{2}-\frac{3x^{2}}{4}\bigg)dx\\=\bigg[\frac{1}{2}\bigg(\frac{3x^{2}}{2}+12x\bigg)-\frac{3x^{3}}{4×3}\bigg]^{4}_{\normalsize-2}\\=\bigg[\frac{3x^{2}}{4}+6x-\frac{x^{3}}{4}\bigg]^{4}_{\normalsize-2}\\=\frac{3×4^{2}}{4}+6×4-\frac{4^{3}}{4}-\\\bigg[\frac{3×4}{4}-12+\frac{8}{4}\bigg]$$
= 12 + 24 – 16 – 3 + 12 – 2 = 27 sq unit.
8. Find the area of the smaller region bounded by
$$\textbf{the ellipse\space}\frac{\textbf{x}^{\textbf{2}}}{\textbf{9}}+\frac{\textbf{y}^{\textbf{2}}}{\textbf{4}}\textbf{= 1}\space\\\textbf{and the line}\frac{\textbf{x}}{\textbf{3}}\textbf{+}\frac{\textbf{y}}{\textbf{2}}\textbf{= 1.}$$
Sol. Given the curve [represents an ellipse with centre at (0, 0)]

$$\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\space\text{...(i)}\\\text{and equation of line}\\\frac{x}{3}+\frac{y}{2}=1\space\text{...(ii)}$$
For the points of intersection of ellipse and line put the value of x from Eq. (ii) in Eq. (i), we get
$$\bigg(\frac{y}{2}-1\bigg)^{2} + \frac{y^{2}}{4}=1.\\\Rarr\space \frac{y^{2}}{4}+1-y+\frac{y^{2}}{4}=1$$
$$\Rarr\space y^{2}-2y=0\Rarr\space y=0,2$$
When y = 0, x = 3 and y = 2, x = 0
i.e., intersection points are A(3, 0) and B(0, 2).
∴ Required area
$$=\space\text{(Area under the curve)}\space\frac{x^{2}}{9}+\frac{y^{2}}{4}=1,\\\text{between x = 0 and x = 3) – }\\\text{(Area under the line}\space\frac{x}{3}+\frac{y}{2}=1,\\\text{between x = 0 and x = 3)}\\=\int^{3}_{0}2\sqrt{1-\frac{x^{2}}{9}dx}-\int^{3}_{0}2\bigg(1-\frac{x}{3}\bigg)dx\\=\frac{2}{3}\int^{3}_{0}\sqrt{3^{2}-x^{2}}dx-\frac{2}{3}\int^{3}_{0}(3-x)dx\\=\frac{2}{3}\bigg[\frac{x}{2}\sqrt{3^{2}-x^{2}+}\space\frac{9}{2}\text{sin}^{\normalsize-1}\frac{x}{3}\bigg]^{3}_{0}-\\\frac{2}{3}\bigg[3x-\frac{x^{2}}{2}\bigg]^{3}_{0}$$
$$\begin{bmatrix}\because\space\int\sqrt{a^{2}-x^{2}}dx=\frac{x}{2}\sqrt{a^{2}-x^{2}}+\\\frac{a^{2}}{2}\text{sin}^{\normalsize-1}\frac{x}{a}\end{bmatrix}\\=\frac{2}{3}\bigg[0+\frac{9}{2}\text{sin}^{\normalsize-1}(1)-0\bigg]-\frac{2}{3}\bigg[9-\frac{9}{2}-0\bigg]\\=3\bigg(\frac{\pi}{2}\bigg)-(3)\\= 3\bigg(\frac{\pi}{2}-1\bigg)\\=\frac{3}{2}(\pi-2)\space\text{sq. unit}$$
9. Find the area of the smaller region bounded by the ellipse
$$\frac{\textbf{x}^{\textbf{2}}}{\textbf{a}^{\textbf{2}}}\textbf{+}\frac{\textbf{y}^{\textbf{2}}}{\textbf{b}^{\textbf{2}}}\textbf{= 1}\space\textbf{and the line}\space\frac{\textbf{x}}{\textbf{a}}+\frac{\textbf{y}}{\textbf{b}}\textbf{=1}.$$
Sol. Given the curve
$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\space\text{...(i)}$$
and equation of line
$$\frac{x}{a}+\frac{y}{b}=1\space\text{...(ii)}$$
On putting the value of x/a from Eq. (ii) in Eq. (i), we get

$$\bigg(1-\frac{y}{b}\bigg)^{2} + \frac{y^{2}}{b^{2}}=1\\\Rarr\space 1 + 2 \bigg(\frac{y^{2}}{b^{2}}\bigg)-\frac{2y}{b}=1\\\Rarr\space \frac{2y}{b}\bigg(\frac{y}{b}-1\bigg)=0$$
$$\Rarr\space y=0, y=b\space\text{then\space x=a, x=0}$$
i.e., the intersection points are A(a, 0) and B(0, b).
The required area is shown in the shaded figure. For the ellipse,
$$\frac{y^{2}}{b^{2}} = 1-\frac{x^{2}}{a^{2}}\\\Rarr\space |y|=\frac{b}{a}\sqrt{a^{2}-x^{2}}\\\text{Now, area of} \Delta \text{AOB}=\frac{1}{2}.|\text{OA}|.|\text{OB}|\\=\frac{1}{2}\space\text{ab\space Sq.unit}$$
Also, area under the ellipse in the first quadrant
$$=\int^{a}_{0}\space\text{y dx}\\=\int^{a}_{0}\frac{b}{a}\sqrt{a^{2}-x^{2}}dx\\=\frac{b}{a}\bigg[\frac{x\sqrt{a^{2}-x^{2}}}{2}+\frac{a^{2}}{2}\text{sin}^{\normalsize-1}\frac{x}{a}\bigg]^{a}_{0}\\=\frac{b}{2a}\lbrack(0 + a^{2}\text{sin}^{\normalsize-1}(1)) - (0 + a^{2}\text{sin}^{\normalsize-1}(0))\rbrack\\=\frac{b}{2a}\bigg[a^{2}.\frac{\pi}{2}-a^{2}.0\bigg]=\frac{\pi ab}{4}\text{sq unit}$$
∴ Required area
= Area of shaded region
= Area of curve OABO – Area of ΔOAB
$$=\frac{\pi ab}{4}-\frac{1}{2}\text{ab}\\=\frac{(\pi-2)ab}{4}\\=\frac{ab}{4}(\pi-2)\text{Sq.\space unit}$$
10. Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the X-axis.
Sol. Given the curve [represent an upward parabola with vertex (0, 0)]
y = x2 ...(i)
and equation of the line
y = x + 2 ...(ii)

The line and parabola meet where x2 = x + 2 (Eliminating y)
∴ x2 – x – 2 = 0
$$\Rarr\space (x-2)(x+1)=0\\\Rarr\space x=2\space\text{or -1}$$
When x = 2, y = 2 + 2 = 4
When x = – 1, y = (– 1) + 2 = 1
Thus, the point of intersection of the parabola and line are (– 1, 1) and (2, 4).
Required area
= (Area under the line y = x + 2, between x = – 1, x = 2) – (Area under the curve x2 = y, between x = – 1, x = 2)
$$=\int^{2}_{\normalsize-1}(x+2)dx-\int^{2}_{\normalsize-1}x^{2}dx\\=\bigg[\frac{x^{2}}{2} + 2x\bigg]^{2}_{\normalsize-1}-\bigg[\frac{x^{3}}{3}\bigg]^{2}_{\normalsize-1}\\=\bigg[\frac{2^{2}}{2}+2×2\bigg]-\bigg[\frac{(\normalsize-1)^{2}}{2} + 2(\normalsize-1)\bigg]-\\\frac{1}{3}\bigg[(2^{3} - (\normalsize-1)^{3})\bigg]\\=6-\frac{1}{2}+2-3=\frac{9}{2}\text{sq unit}$$
11. Using method of integration find the area bounded by the curve |x| + |y| = 1.
[Hint : The required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 1]
Sol. The given curve is |x| + |y| = 1
In first quadrant, (x > 0, y > 0)
Then, the line
AB is x + y = 1

In second quadrant, (x < 0, y > 0)
Then, the line BC is – x + y = 1
In third quadrant (x < 0, y < 0)
Then, the line CD is – x – y = 1
In fourth quadrant (x > 0, y < 0)
Then, the line DA is x – y = 1
Since, ABCD is a square.
∴ Required area
= 4 (Area of shaded region in the first quadrant)
$$= 4\int^{1}_{0}(1-x)dx\\(\because\space x+y=1\Rarr\space y=1-x)\\=4\bigg[x-\frac{x^{2}}{2}\bigg]^{1}_{0}\\= 4\bigg[\bigg(1-\frac{1}{2}\bigg)-0\bigg]=\text{2 sq. unit.}$$
12. Find the area bounded by curves
$$\lbrace\textbf{(x,y) : y}\ge \textbf{x}^{\textbf{2}}\space\textbf{and}\space \textbf{y = |x|}\rbrace $$
Sol. Given the curve
y = x2 ...(i)
and equation of line
y = |x| ...(ii)
In first quadrant, the equation of the line is y = x and in second quadrant, the equation of line is y = – x.
The points of intersection of the parabola and line are (– 1, 1) and (1, 1). As the area to be found is symmetrical about Y-axis.

∴ Required area
= 2(Area of shaded region in the first quadrant)
$$= 2\int^{1}_{0}(x-x^{2})dx\\= 2\bigg[\int^{1}_{0}x dx - \int^{1}_{0}\space x^{2}dx\bigg]\\= 2\bigg(\bigg[\frac{x^{2}}{2}\bigg]^{1}_{0}-\bigg[\frac{x^{3}}{3}\bigg]^{1}_{0}\bigg)\\=2\bigg[\bigg(\frac{1}{2}-0\bigg)-\bigg(\frac{1}{3}-0\bigg)\bigg]\\= 2\bigg[\frac{1}{2}-\frac{1}{3}\bigg]=2\bigg[\frac{1}{6}\bigg]=\frac{1}{3}\text{sq.unit}$$
13. Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B(4, 5) and C(6, 3).
Sol. The given points are A(2, 0), B(4, 5) and C(6, 3)
Equation of line AB is
$$y-0=\frac{5-0}{4-2}(x-2)\\\bigg[\text{Using y-y}_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\bigg]\\\Rarr\space y=\frac{5}{2}x-5\\\text{Equation of line BC is}\\\text{y-5}=\frac{3-5}{6-4}(x-4)\\\Rarr\space y= -x+9$$
Equation of line AC is
$$y-0 = \frac{3-0}{6-2}(x-2)\\\Rarr\space y=\frac{3}{4}x-\frac{3}{2}$$

Required area = (Area under line segment AB) + (Area under line segment BC) – (Area under line segment AC)
$$=\int^{4}_{2}\bigg(\frac{5}{2}x-5\bigg)dx+\int^{6}_{4}(-x+9)dx-\\\int^{6}_{2}\bigg(\frac{3}{4}x-\frac{3}{2}\bigg)dx\\=\bigg[\frac{5x^{2}}{4}-5x\bigg]^{4}_{2} + \bigg[\frac{-x^{2}}{2} + 9x\bigg]^{6}_{4}-\\\bigg[\frac{3x^{2}}{8}-\frac{3}{2}x\bigg]^{6}_{2}\\=\bigg[\bigg(\frac{5×4^{2}}{4}-5×4\bigg)- \bigg(\frac{5×2^{2}}{4}-5×2\bigg)\bigg]+\\\bigg[\bigg(\frac{-6^{2}}{2}+9×6\bigg) - \bigg(\frac{-4^{2}}{2}+9×4\bigg)\bigg]-\\$$
$$\bigg(\frac{3×6^{2}}{8}-\frac{3}{2}×6\bigg) + \bigg(\frac{3×2^{2}}{8}-\frac{3}{2}×2\bigg)$$
= (20 – 20) – (5 – 10) + (– 18 + 54) – (– 8 + 36) -
$$\bigg(\frac{27}{2}-9\bigg) + \bigg(\frac{3}{2}×2\bigg)\\= 5+36-28-\frac{9}{2}-\frac{3}{2}=\text{sq. unit.} $$
14. Using the method of integration, find the area of the region bounded by lines
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0.
Sol. The given lines are
2x + y = 4 ...(i)
3x – 2y = 6 ...(ii)
x – 3y + 5 = 0 ...(iii)

From lines equations (i) and (ii), we get
$$4-2x = \frac{3x-6}{2}\space\text{(Eliminating y)}$$
$$\Rarr \text{8 – 4x = 3x – 6}\\ \Rarr 7x = 14 \Rarr x = 2$$
Using equations (i), w e get
y = 4 – 2x = 4 – 2 × 2 = 0
∴ Equations (i) and (ii) intersect at the point (2, 0).
From equations (ii) and (iii), we get
$$\frac{3x-6}{2}=\frac{x+5}{3}\\\Rarr\space 9x-18 = 2x+10\\\Rarr\space 7x+28\Rarr x=4$$
Using equation (ii), we get
$$y=\frac{3×4-6}{2}=3$$
∴ Equations (ii) and (iii) intersect at the point (4, 3).
From lines equations (i) and (iii), we get
$$4-2x = \frac{x+5}{3}\\\Rarr\space 7x=7\Rarr\space x=1$$
Using equation (i), we get
y = 4 – 2x = 4 – 2 × 1 = 2
Equations (i) and (iii) intersect at the point (1, 2).
∴ Required area
= (Area under line segment BA ) – (Area under line segment BC) – (Area under line segment AC)
$$=\int^{4}_{1}\bigg(\frac{x+5}{3}\bigg)dx-\int^{2}_{1}(4-2x)dx -\\ \int^{4}_{2}\bigg(\frac{3x-6}{2}\bigg)dx\\=\frac{1}{3}\bigg[\frac{(x+5)^{2}}{2}\bigg]^{4}_{1}-\bigg[4x-x^{2}\bigg]^{2}_{1}-\\\frac{1}{2}\bigg[\frac{3x^{2}}{2}-6x\bigg]^{4}_{2}\\=\frac{1}{6}[9^{2}-6^{2}]-\lbrace(8-4)-(4-1)\rbrace\\-\frac{1}{2}\bigg[\bigg(\frac{3×4^{2}}{2}-6×4\bigg)-\bigg(3×\frac{2^{2}}{2}-6×2\bigg)\bigg]$$
$$=\frac{45}{6}-1-\frac{1}{2}(0-6+12)\\=\frac{15}{2}-1-3=\frac{7}{2}\text{sq unit}$$
15. Find the area of the region
$$\lbrace\textbf{(x,y) : y}^{\textbf{2}}\leq \textbf{4x, 4x}^{\textbf{2}}\textbf{ + 4y}^{\textbf{2}}\leq \textbf{9}\rbrace.$$
Sol. Given curve
y2 = 4x ...(i)
and circle
4x2 + 4y2 = 9 ...(ii)
Which represents a circle whose centre is (0, 0)
$$\text{and radius}\space\frac{3}{2}.$$

For intersecting points of parabola and circle put the value of y2 from Eq. (i) in Eq. (ii), we get
4x2 + 16x = 9
$$\Rarr\space\text{4x}^{2} + 16x - 9=0\\\Rarr\space 4x^{2}+18x-2x-9=0\\\Rarr\space 2x(2x+9)-1(2x+9)=0\\\Rarr\space(2x+9)(2x-1)=0\\\Rarr\space x=\frac{-9}{2},\frac{1}{2}\\\Rarr\space x=\frac{1}{2}\\\bigg( x\neq\frac{-9}{2}\space\text{because it does not satisfy}\\\text{the given inequality}\bigg)\\\text{On putting x =}\frac{1}{2}\space\text{in Eq.(i),}\\ \text{we get y =}\pm\sqrt{2}$$
∴ The points of intersection of both the curves are
$$\text{A}\bigg(\frac{1}{\sqrt{2}},\sqrt{2}\bigg)\space\text{and}\space\text{C}\bigg(\frac{1}{2},-\sqrt{2}\bigg).$$
Since, the shaded region is symmetrical about X-axis.
∴ Required area
= 2 (Area OABO)
$$= 2\bigg[\int^{\frac{1}{2}}_{0}\sqrt{4x}dx + \int^{\frac{3}{2}}_{\frac{1}{2}}\sqrt{\frac{9-4x^{2}}{4}}dx\bigg]\\= 2×2\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{\frac{1}{2}}_{0} + 2\int^{\frac{3}{2}}_{\frac{1}{2}}\sqrt{\bigg(\frac{3}{2}\bigg)^{2}-x^{2}}dx\\=\frac{8}{3}\bigg[\bigg(\frac{1}{2}\bigg)^{\frac{3}{2}}-0\bigg]+\\2\bigg[\frac{x}{2}\sqrt{\frac{9}{4}-x^{2}}+ \frac{9}{8}\text{sin}^{\normalsize-1}\frac{x}{\frac{3}{2}}\bigg]^{\frac{3}{2}}_{\frac{1}{2}}\\=\frac{8}{3}.\frac{1}{2\sqrt{2}}+2\begin{bmatrix}0+\frac{9}{8}\text{sin}^{\normalsize-1}(1)-\\\frac{1}{4}\sqrt{\frac{9}{4}-\frac{1}{4}}-\frac{9}{8}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg)\end{bmatrix}$$
$$= \frac{2\sqrt{2}}{3}+\frac{9}{4}.\frac{\pi}{2}-\frac{\sqrt{2}}{2}-\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{1}{3}\bigg)\\=\frac{9\pi}{8}+\frac{\sqrt{2}}{6}-\frac{9}{4}\text{sin}^{\normalsize-1}\frac{1}{3}\\=\frac{9\pi}{8} + \frac{1}{3\sqrt{2}}-\frac{9}{4}\text{sin}^{\normalsize-1}\frac{1}{3}$$
Choose the correct answer.
16. Area bounded by the curve y = x3, the X-axis and the coordinates x = – 2 and x = 1 is :
$$\textbf{(a)\space -9}\space\\\textbf{(b)\space}\textbf{-}\frac{\textbf{15}}{\textbf{4}}\\\textbf{(c)\space}\frac{\textbf{15}}{\textbf{4}}\\\textbf{(d)\space}\frac{\textbf{17}}{\textbf{4}}\\\textbf{Sol.\space}\text{(d)\space}\frac{17}{4}$$
Given curve is y = x3
On putting x = – x and y = – y, we get y = x3
Therefore, the curve is symmetrical in opposite quadrant and passes through (0, 0).

∴ Required area
$$=\int^{1}_{\normalsize-2}|x^{3}|dx\\=\int^{0}_{\normalsize-2}|x^{3}|dx + \int^{1}_{0}|x^{3}|dx\\=\int^{0}_{-2}(-x^{3})dx + \int^{1}_{0}x^{3}dx\\\bigg[\because\space |x^{3}|=\begin{Bmatrix}x^{3}, \space \text{if x}\geq 0\\-x^{3},\space \text{if x}\text{\textless} 0\end{Bmatrix}\bigg]\\=-\bigg[\frac{x^{4}}{4}\bigg]^{0}_{\normalsize-2} + \bigg[\frac{x^{4}}{4}\bigg]^{1}_{0}\\=-\bigg[0-\frac{(-2)^{4}}{4}\bigg] + \bigg[\frac{1}{4}-0\bigg]\\=-(\normalsize-4)+\bigg(\frac{1}{4}\bigg)=\frac{17}{4}\text{sq unit}$$
17. The area bounded by the curve y = x |x|, X-axis and the coordinates x = – 1 and x = 1 is given by
(a) 0
$$\textbf{(b)\space}\frac{\textbf{1}}{\textbf{3}}\\\textbf{(c)\space}\frac{\textbf{2}}{\textbf{3}}\\\textbf{(d)\space}\frac{\textbf{4}}{\textbf{3}}\\\textbf{Sol.\space}\text{(c)}\frac{2}{3}\\\text{Given\space} y=x|x|=\begin{cases}x^{2}, x\geq0\\-x^{2}, x\text{\textless}0\end{cases}$$

Required area
= 2 [Area under the curve y = x2, between x = 0, x = 1
[∵ The curve is symmetrical in opposite quadrant.]
$$= 2 \int^{1}_{0}x|x| = 2\int^{1}_{0}x^{2}dx\\= 2\bigg[\frac{x^{3}}{3}\bigg]^{1}_{0}=\frac{2}{3}(1^{3}-0^{3})\\=\frac{2}{3}\text{sq unit}$$
18. The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is :
$$\textbf{(a)\space}\frac{\textbf{4}}{\textbf{3}}\textbf{(4}\pi - \sqrt{\textbf{3}})\\\textbf{(b)\space}\frac{\textbf{4}}{\textbf{3}}(\textbf{4}\pi \textbf{+} \sqrt{\textbf{3}})\\\textbf{(c)\space}\frac{\textbf{4}}{\textbf{3}}\textbf{(8} - \sqrt{\textbf{3}})\\\textbf{(d)\space}\frac{\textbf{4}}{\textbf{3}}\textbf{(8}\pi + \sqrt{\textbf{3}})\\\textbf{Sol.\space}\text{(c)}\space\frac{4}{3}(8\pi - \sqrt{3})$$
The circle x2 + y2 = 16 and the parabola y2 = 6x meet where
x2 + 6x = 16 (Eliminating y)
$$\Rarr\space x^{2}+6x-16 = 0\\\Rarr\space (x+8)(x-2)=0\\\Rarr\space x=-8,2$$

∴ Required area
= Area of the circle – 2 × Area shown in the shaded region.
$$=\pi(4)^{2}-2\bigg[\int^{2}_{0}\sqrt{6x} + \int^{4}_{2}\sqrt{16-x^{2}}dx\bigg]\\= 16\pi-2\sqrt{6}\bigg[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\bigg]^{2}_{0}-\\2\bigg[\frac{x}{2}\sqrt{16-x^{2}}+\frac{16}{2}\text{sin}^{\normalsize-1}\frac{x}{4}\bigg]^{4}_{2}\\=16\pi-\frac{4\sqrt{6}}{3}(2^{\frac{3}{2}}-0)-\\2\bigg[0+8\text{sin}^{\normalsize-1}(1) -\sqrt{16-4}-8\text{sin}^{\normalsize-1}\frac{1}{2}\bigg]$$
$$= 16\pi-\frac{4\sqrt{6}×2\sqrt{2}}{3}-\\2\bigg[8×\frac{\pi}{2}-\sqrt{12}-8×\frac{\pi}{6}\bigg]\\=16\pi - \frac{8\sqrt{12}}{3}-8\pi+2\sqrt{12} + \frac{8\pi}{3}\\= 16\pi-\frac{16\sqrt{3}}{3}-\frac{16\pi}{3}+4\sqrt{3}\\=\frac{32\pi}{3}-\frac{4\sqrt{3}}{3}\\=\frac{4}{3}(8\pi-\sqrt{3})\text{sq unit} $$
19. The area bounded by the Y-axis, y = cos x and
$$\textbf{y = sin x when 0}\leq x\leq\frac{\pi}{\textbf{2}}\textbf{is :}\\\textbf{(a)\space 2}\textbf{(}\sqrt{\textbf{2}}\textbf{-1)}\\\textbf{(b)\space}\sqrt{\textbf{2}}\textbf{-1}\\\textbf{(c)\space}\sqrt{\textbf{2}}\textbf{+1}\\\textbf{(d)\space}\sqrt{\textbf{2}}\\\textbf{Sol.\space}\sqrt{2}-1$$
The two curves y = sin x and y = cos x meet where sin x = cos x, i.e., where tan x = 1.
$$\Rarr\space x=\frac{\pi}{4}$$

∴ Required area (shown in shaded region)
$$=\int^{\frac{\pi}{4}}_{0}(\text{cos x - sin x})dx-[\text{sin x + cos x}]^{\frac{\pi}{4}}_{0}\\=\text{sin}\frac{\pi}{4}+\text{cos}\frac{\pi}{4}-(0+1)\\=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-1\\=\frac{2}{\sqrt{2}}-1=\sqrt{2}-1.$$
