NCERT Solutions for Class 12 Maths Chapter 8 - Applications of Integrals - Exercise 8.2



Access Exercises of Class 12 Maths Chapter 8 – Applications of the Integrals
Exercise 8.1 Solutions: 13 Questions (8 Long, 3 Short, 2 MCQs)
Exercise 8.2 Solutions: 7 Questions(5 Long, 2 MCQs)
Miscellaneous Exercise Solutions: 19 Questions (8 Long, 7 Short, 4 MCQs)
Exercise 8.2
1. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
Sol. Given, circle is 4x2 + 4y2 = 9 and the given parabola is x2 = 4y. The two curves meet where
4(4y) + 4y2 = 9
$$\Rarr\space 4y^{2} + 16y-9=0\\\Rarr\space y=\frac{-16\pm\sqrt{256 + 144}}{2×4}\\=\frac{-16\pm\sqrt{400}}{8}=\frac{-16\pm 20}{8}\\=\frac{1}{2},-\frac{9}{2}\\\text{But y}\gt0,\space\text{therefore, the two curves}\\\text{meet when y =}\frac{1}{2}.$$

$$\text{i.e.,\space when}\space x^{2}=4×\frac{1}{2}=2,\\\text{i.e.,\space when x = }\pm\sqrt{2}.$$
∴ Required area (shown in shaded region)
$$= 2\int^{\sqrt{2}}_{0}(y_2-y_1)dx\\= 2\begin{Bmatrix}\int^{\sqrt{2}}_{0}\sqrt{\frac{9-4x^{2}}{4}}dx - \int^{\sqrt{2}}_{0}\frac{x^{2}}{4}dx\end{Bmatrix}\\= 2\int^{\sqrt{2}}_{0}\sqrt{\bigg(\frac{3}{2}\bigg)^{2}-x^{2}}dx - \frac{2}{4}\bigg[\frac{x^{3}}{3}\bigg]^{\sqrt{2}}_{0}\\= 2\bigg[\frac{x}{2}\sqrt{\bigg(\frac{3}{2}\bigg)^{2}-x^{2}} + \frac{(\frac{3}{2})^{2}}{2}\text{sin}^{\normalsize-1}\bigg(\frac{x}{3/2}\bigg)\bigg]^{\sqrt{2}}_{0}\\-\frac{1}{6}\lbrack(\sqrt{2})^{3}-0\rbrack$$
$$=\bigg[x\sqrt{\frac{9}{4}-x^{2}} + \frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{2x}{3}\bigg)\bigg]^{\sqrt{2}}_{0}-\\\frac{2\sqrt{2}}{6}\\=\bigg[\sqrt{2}\sqrt{\frac{9}{4}-2}+\frac{9}{4}\text{sin}^{-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)\bigg]-\\\lbrack0-0\rbrack-\frac{2\sqrt{2}}{6}\\=\frac{\sqrt{2}}{2}+\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)-\frac{2\sqrt{2}}{6}\\=\bigg(\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{3}\bigg)+\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)\\=\frac{\sqrt{2}}{6}+\frac{9}{4}\text{sin}^{\normalsize-1}\bigg(\frac{2\sqrt{2}}{3}\bigg)\text{sq unit}$$
2. Find the area bounded by the curves (x – 1)2 + y2 = 1 and x2 + y2 = 1.
Sol. Given, curve (x – 1)2 + y2 = 1 ...(i)
$$\therefore\space y=\sqrt{ 1- (x-1)^{2}}$$
which represents a circle with centre (1, 0) and radius 1
and curve x2 + y2 = 1 ...(ii)

$$\therefore\space y=\sqrt{1-x^{2}}$$
which represents a circle with centre (0, 0) and radius 1.
Both the curves are circle and meet where (x – 1)2 = x2 i.e., where 2x = 1 or $$x = \frac{1}{2}.$$
Required area (shown in shaded region).
$$= 2\bigg[\int^{\frac{1}{2}}_{0}y_1 dx + \int^{1}_{\frac{1}{2}}y_2 dx\bigg]\\=2\begin{Bmatrix}\int^{\frac{1}{2}}_{0}\sqrt{1 - (x-1)^{2}}dx + \\\int^{1}_{\frac{1}{2}}\sqrt{1-x^{2}}dx\end{Bmatrix}\\=2 \begin{bmatrix}\frac{x-1}{2}\sqrt{1 -(x-1)^{2}} + \frac{1}{2}\text{sin}^{\normalsize-1}\frac{x-1}{1}\end{bmatrix}^{\frac{1}{2}}_{0}+\\2\bigg[\frac{x}{2}\sqrt{1-x^{2}}+\frac{1}{2}\text{sin}^{\normalsize-1}x\bigg]^{1}_{\frac{1}{2}}$$
$$=2\begin{bmatrix}\frac{\frac{1}{2}-1}{2}\sqrt{1-\frac{1}{4}} + \frac{1}{2}\text{sin}^{\normalsize-1}\bigg(-\frac{1}{2}\bigg)-\\\bigg(\frac{-1}{2}\bigg)0-\frac{1}{2}\text{sin}^{\normalsize-1}(\normalsize-1)\end{bmatrix}+\\2\begin{bmatrix}0+\frac{1}{2}\text{sin}^{\normalsize-1}(1) - \\\frac{1}{4}\sqrt{1-\frac{1}{4}}-\frac{1}{2}\text{sin}^{\normalsize-1}\frac{1}{2}\end{bmatrix}$$
$$= 2\bigg[-\frac{1}{4}.\frac{\sqrt{3}}{2}-\frac{1}{2}.\frac{\pi}{6} + 0 + \frac{1}{2}.\frac{\pi}{2}\bigg]+\\\frac{\pi}{2}-\frac{1}{2}.\frac{\sqrt{3}}{2}-\frac{\pi}{6}\\=-\frac{\sqrt{3}}{4}-\frac{\pi}{6} + \frac{\pi}{2}+\frac{\pi}{2}-\frac{\sqrt{3}}{4}-\frac{\pi}{6}\\=\bigg(\frac{2\pi}{3} - \frac{\sqrt{3}}{2}\bigg)\text{sq unit}$$
3. Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3.
Sol. Given curve y = x2 + 2 represents a parabola and it is symmetrical about Y-axis having vertex (0, 2).

The given region bounded by y = x2 + 2, y = x, x = 0 and x = 3, is represented by the shaded area.
The point of intersection of the curve y = x2 + 2 and the line x = 3 is (3, 11).
Required area (shown is shaded region)
= Area OABDO – Area OCDO
= [Area under y = x2 + 2 between x = 0, x = 3] – [Area under y = x between x = 0, x = 3]
$$=\int^{3}_{0}(x^{2}+2)dx - \int^{3}_{0} xdx\\=\bigg[\frac{x^{3}}{3}+2x\bigg]^{3}_{0}-\bigg[\frac{x^{2}}{2}\bigg]^{3}_{0}\\=\bigg[\frac{3^{3}}{3}+6-0\bigg]-\bigg[\frac{3^{2}}{2}-0\bigg]\\=9+6-\frac{9}{2}=\frac{21}{2}\text{sq unit}$$
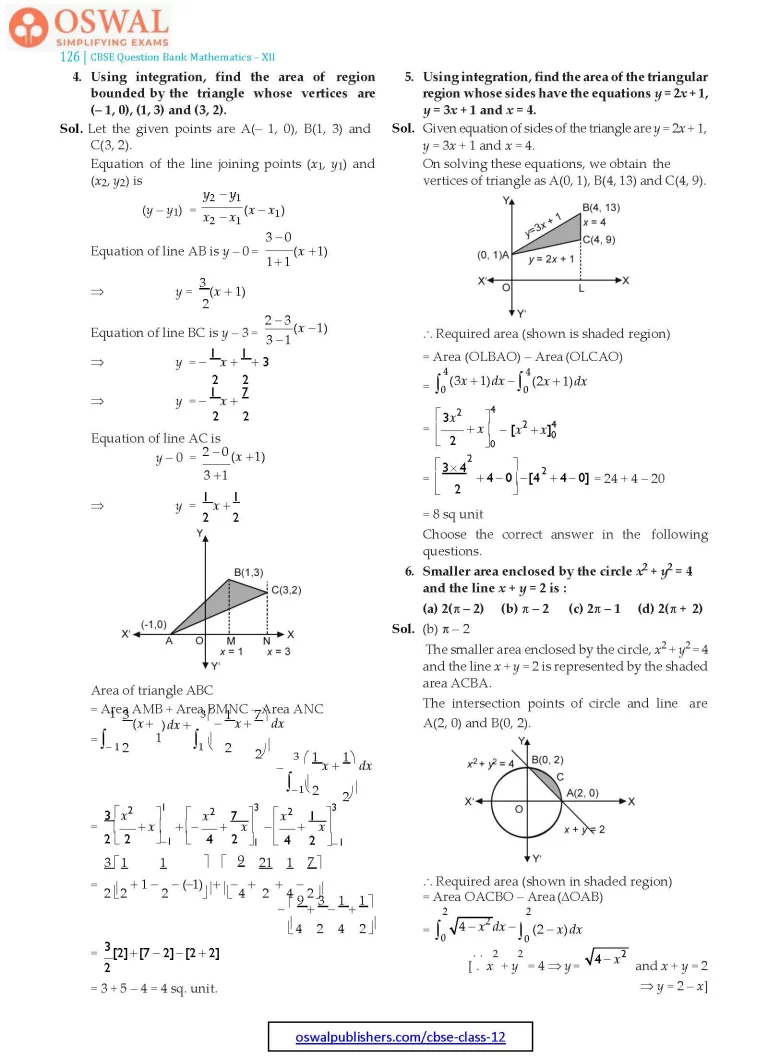
4. Using integration, find the area of region bounded by the triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).
Sol. Let the given points are A(– 1, 0), B(1, 3) and C(3, 2).
Equation of the line joining points (x1, y1) and (x2, y2) is
$$(y-y_1)=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\\\text{Equation of line AB is y – 0 }\\=\frac{3-0}{1+1}(x+1)\\\Rarr\space y=\frac{3}{2}(x+1)\\\text{Equation of line BC is y – 3 =}\\\frac{2-3}{3-1}(x-1)\\\Rarr\space y=-\frac{1}{2}x+\frac{1}{2}+3\\\Rarr\space y=-\frac{1}{2}x+\frac{7}{2}\\\text{Equation of line AC is}\\\text{y-0}=\frac{2-0}{3+1}(x+1)$$
$$\Rarr\space y=\frac{1}{2}x+\frac{1}{2}$$

Area of triangle ABC
= Area AMB + Area BMNC – Area ANC
$$=\int^{1}_{-1}\frac{3}{2}(x+1)dx + \int^{3}_{1}\bigg(-\frac{1}{2}x+\frac{7}{2}\bigg)dx-\\\int^{3}_{\normalsize-1}\bigg(\frac{1}{2}x+\frac{1}{2}\bigg)dx\\=\frac{3}{2}\bigg[\frac{x^{2}}{2}+x\bigg]^{1}_{\normalsize-1} + \bigg[-\frac{x^{2}}{4}+\frac{7}{2}x\bigg]^{3}_{1}-\\\bigg[\frac{x^{2}}{4}+\frac{1}{2}x\bigg]^{3}_{\normalsize-1}\\=\frac{3}{2}\bigg[\frac{1}{2}+1-\frac{1}{2}-(-1)\bigg] + \\\bigg[-\frac{9}{4}+\frac{21}{2}+\frac{1}{4}-\frac{7}{2}\bigg]-\\\bigg[\frac{9}{4}+\frac{3}{2}-\frac{1}{4}+\frac{1}{2}\bigg]$$
$$=\frac{3}{2}\lbrack2\rbrack + \lbrack7-2\rbrack + \lbrack-2+2\rbrack$$
= 3 + 5 – 4 = 4 sq. unit.
5. Using integration, find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
Sol. Given equation of sides of the triangle are y = 2x + 1, y = 3x + 1 and x = 4.
On solving these equations, we obtain the vertices of triangle as A(0, 1), B(4, 13) and C(4, 9).

∴ Required area (shown is shaded region)
= Area (OLBAO) – Area (OLCAO)
$$=\int^{4}_{0}(3x+1)dx-\int^{4}_{0}(2x+1)dx\\=\bigg[\frac{3x^2}{2}+x\bigg]^{4}_{0}-\lbrack x^{2}+x\rbrack^{4}_{0}\\=\bigg[\frac{3×4^{2}}{2}+4-0\bigg]-\lbrack 4^{2}+4-0\rbrack\\=24+4-20$$
= 8 sq unit
Choose the correct answer in the following questions.
6. Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is :
$$\textbf{(a)\space}\textbf{2(}\pi\textbf{-2)}\\\textbf{(b)\space}\pi\textbf{- 2}\\\textbf{(c)\space}\textbf{2}\pi\textbf{- 1}\\\textbf{(d)\space}\textbf{2(}\pi + \textbf{2)}\\\textbf{Sol.}\space\text{(b)}\space \pi-2$$
The smaller area enclosed by the circle, x2 + y2 = 4 and the line x + y = 2 is represented by the shaded area ACBA.
The intersection points of circle and line are A(2, 0) and B(0, 2).

∴ Required area (shown in shaded region)
= Area OACBO – Area (ΔOAB)
$$=\int^{2}_{0}\sqrt{4-x^{2}}dx - \int^{2}_{0}(2-x)dx\\\lbrack\because x^{2}+y^{2}=4\\\Rarr\space y=\sqrt{4-x^{2}\space}\text{and x+y=2}\\\Rarr\space y=2-x\rbrack$$
$$=\bigg[\frac{x}{2}\sqrt{4-x^{2}} + \frac{4}{2}\text{sin}^{\normalsize-1}\frac{x}{2}\bigg]^{2}_{0}-\\\bigg[2x-\frac{x^{2}}{2}\bigg]^{2}_{0}$$
$$=\bigg[\frac{2}{2}\sqrt{4-4} + \frac{4}{2}\text{sin}^{\normalsize-1}(1) - 0- \frac{4}{2}\text{sin}^{\normalsize-1}(0)\bigg]-\\\lbrack4-2\rbrack$$
$$\begin{bmatrix}\because\space \int\sqrt{a^{2}-x^{2}}dx =\frac{x}{2}\sqrt{a^{2}-x^{2}} +\\\frac{a^{2}}{2}\text{sin}^{\normalsize-1}\frac{x}{a}\end{bmatrix}\\=\begin{bmatrix}2.\frac{\pi}{2}\end{bmatrix}-[4-2]=(\pi-2)\text{sq.unit.}$$
7. Area lying between the curves y2 = 4x and y = 2x is :
$$\textbf{(a)\space}\frac{\textbf{2}}{\textbf{3}}\\\textbf{(b)\space}\frac{\textbf{1}}{\textbf{3}}\\\textbf{(c)\space}\frac{\textbf{1}}{\textbf{4}}\\\textbf{(d)\space}\frac{\textbf{3}}{\textbf{4}}\\\textbf{Sol.}\space\text{(b)}\frac{1}{3}$$
The given curve is y2 = 4x ...(i)
and the given line is y = 2x ...(ii)
The two curve meet where (2x)2 = 4x
$$\Rarr\space 4x(x-1)=0\\\Rarr\space x=0,1$$
When x = 0, y = 2 × 0 = 0
and when x = 1, y = 2 × 1 = 2
∴ Equations (i) and (ii) meet at the points (0, 0) and (1, 2).

$$\text{Required area =}\int^{1}_{0}(2\sqrt{x} -2x)dx\\(\because\space y^{2}=4x\Rarr\space |y|=2\sqrt{x})\\=\bigg[2\frac{x^{\frac{3}{2}}}{\frac{3}{2}}-x^{2}\bigg]^{1}_{0}\\=\frac{4}{3}.1^{\frac{3}{2}}-1^{2}=0\\=\frac{1}{3}\text{sq unit}$$
